期待効用理論

今回紹介するのは「サンクトペテルブルクのパラドックス」というものです。 長い名前ですね。 いまコイン投げをして、何回目に初めて表が出たかによって賞金がもらえます。 n 回目に初めて表が出たとき、 2n 万円もらえるとします。 でもこのゲームには参加料がいります。あなたなら、どれくらいの参加料までならこのゲームをしますか？ これは簡単ですね。今まで通り期待値を計算して、その期待値を少し下回るぐらいの金額を参加料の上限とすればいいわけです。それではさっそく計算しましょう。 コインの表が出る確率は 1/2 です。n 回目に初めて表が出る確率は、 n-1 回目まで裏が出続けて、n 回目に表が出るということですから、 (1/2)n-1(1/2) = (1/2)n この n を 1 から無限大まで考えればよいのですね。 そして、それぞれでもらえる賞金は 2n 万円。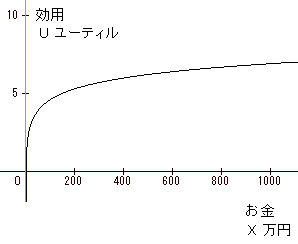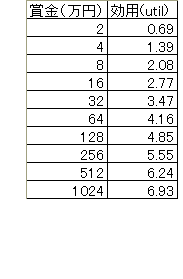 よって期待値は (1/2)121 + (1/2)222 + ・・・ + (1/2)n2n + ・・・ = 1 + 1 + ・・・ + 1 + ・・・・ = ∞ （万円） なるほど、期待値は無限大。じゃあこのゲームは1兆円払ってでもやる価値がありますね・・・。 うーん、何か変ですね・・・。 これがサンクトペテルブルクのパラドックスです。 ものすごく小さい確率だけど、 いくらでも大きい額をもらえる可能性があるので、期待値が無限大に発散してしまうのです。 このパラドックスは、期待値がゲームの評価基準としてもっともらしくないことを示唆しています。 何かいい解決法はないでしょうか。 そういえばミクロ経済学には「限界効用逓減」という考え方があった気がします。 もらえるお金が増えても、主観的な評価はそれに比例して大きくなるのではなく、 もらえるお金が増えるにつれて、だんだんうれしくなくなってくるという考え方ですね。 そしてそれは対数関数のようなグラフで表されていました。 賞金が512万円から1024万円に512万円増えても、 賞金が16万円から32万円に16万円増えるのとうれしさは変わらない、というように、 うれしさが鈍化していくのですね。 そこで、 ゲームを客観的なお金じゃなくて主観的な効用で考えてみることにしましょう。 プレーヤーのお金 X 万円に対する主観的な評価が logeX ユーティル （効用を表す単位）ということにします。 ゲームをユーティルという新しい尺度ではかるのです。

　

ゲームの期待値をユーティルで計算すると M(U) = (1/2)log2 + (1/2)2log22 + ・・・ + (1/2)nlog2n + ・・・ = (1/2 + 2/22 + ・・・ + n/2n + ・・・)log2 = 2log2　・・・(*) = log4 = 1.39 （ユーティル） ということは、せいぜい出すのは1.39ユーティルまでということになります。 これが考えられる参加料です。お金に直すと4万円。 これはなんとなくわかるような気がします。 お金の代わりに効用を考えることで、なんか解決したっぽいです。 このように、 プレーヤーが期待値でなく期待効用で動くとするのが期待効用理論です。 (*) (1/2 + 2/22 + ・・・ + n/2n + ・・・) = 2　について （めんどくさいので Excel で計算したほうが早いです。 n=20 ぐらいまでの和をとってみると 2 に収束することがわかります。 下は参考までに。） まず部分和Snを考えます。 Sn = 1/2 + 2/22 + 3/23 + 4/24 + ・・・ + n/2n = (1/2) + 2(1/2)2 + 3(1/2)3+ 4(1/2)4 + ・・・ + n(1/2)n (1/2)Sn　を作って差をとります。 (1/2)Sn =　　　 　　(1/2)2 + 2(1/2)3 + 3(1/2)4 + ・・・ + (n-1)(1/2)n + n(1/2)n+1 Sn - (1/2)Sn = (1/2) + (1/2)2 + (1/2)3 + (1/2)4 + ・・・ + (1/2)n - n(1/2)n+1 n → ∞　で (1/2)Sn = (1/2)/｛1-(1/2)｝　-　 n(1/2)n+1 = 1 - n(1/2)n+1 また n(1/2)n+1 = n/2n+1 → 0　 よって (1/2)Sn→ 1 Sn → 2 ◆参考文献 『ゲーム理論』　 　 岡田章、有斐閣、1996年