|
1. ゲームの標準型による表現
- 1から n までの番号の付いた n 人のプレーヤーの中の任意の１人をプレーヤー i という。
- プレーヤー i のとりうる戦略の集合を Si で表し、これを i の戦略空間と呼ぶ。
- Si の任意の要素を si と書く。
- (s1,・・・, sn) で各プレーヤーが１つずつ選んだ戦略の組合せを表す。
- ui でプレーヤー i の利得関数を表す。
- ui (s1, ・・・, sn) で
(s1, ・・・, sn) という戦略の組が選ばれたときの
プレーヤー i の利得を表す。
|
定義 n 人ゲームの標準型による表現とは、各プレーヤーの戦略空間
S1, ・・・, Sn および
利得関数 u1, ・・・, un を定めることである。そのゲームは
G = {S1, ・・・, Sn ; u1, ・・・, un} で表される。
|
 ＜ ちんぷんかんぷんれす
 ＜ ほんまや
 ＜ n=2 のときを考えましょう
「2人ゲームの標準型による表現とは、各プレーヤーの戦略空間
S1, S2 および
利得関数 u1, u2 を定めることである。そのゲームは
G = {S1, S2 ; u1, u2} で表される。」
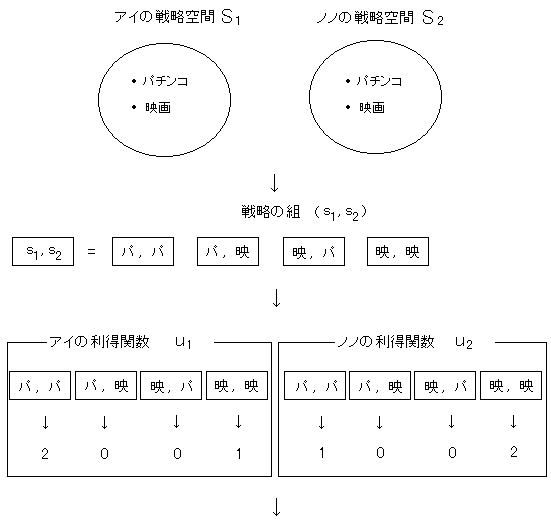
戦略空間 S1 というのは、プレーヤー1のとりうる戦略の集合のことです。
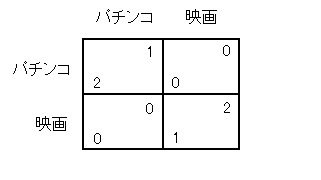
アイの戦略空間は S1={パチンコ、映画} です。
ここで S1 の任意の要素を s1 と書きます。
同様に、戦略空間 S2 というのは、プレーヤー2のとりうる戦略の集合のこと
です。ノノの戦略空間は S2={パチンコ、映画} です。
ここで S2 の任意の要素を s2 と書きます。
u1 (s1, s2) で
(s1, s2) という戦略の組が選ばれたときのプレーヤー1の利得を
表します。 同様に、u2 (s1, s2) で
(s1, s2) という戦略の組が選ばれたときのプレーヤー2の利得を
表します。
 |
テーブルを見てね。
いまテーブルの中の数字がなかったらゲームにならないよね。
アイもノノも４つの戦略の組合せのそれぞれに対応する利得がないとだめだよね。
これが利得関数を定めるってことだよ。
|
|
| かんすうってなんれすか |
|
|
戦略の組って変数だよね。
関数というのはなんか数字を入れると
またなんか数字が出てくる箱のことだったとおもうよ。
だから利得関数というのは戦略の組を入れると利得が出てくる箱のことだね。
アイもノノも自分専用のそういう箱をもってるんだね。
下に図をかいてみたよ。
|
|
| "i" とか「任意の」とかがよくわからへん |
|
|
どれを選んでもいいということだよ。「どのプレーヤーでも」「どの戦略でも」ってことだね。 i に 1 から n まで何でも代入してみていいってことだよ。
|
|
| 標準型による表現では、 n=2 のときは利得行列を用いればよいですが、 n≧3 のときは利得関数を用います。 |
|
ゲームの標準型による表現
