強く支配される戦略

2. 強く支配される戦略 定義　 標準型ゲーム G = {S1, ・・・, Sn ; u1, ・・・, un} を考え、 si' と si'' をプレーヤー i のとりうる戦略であるとする（つまり si' と si'' はともに Si の要素であるとする）。 このとき戦略 si' が戦略 si'' によって強く支配されるとは、他のプレーヤーのどんな可能な戦略の組合せに対しても、 i が si' を選んだときの利得が si'' を選んだときの利得より厳密に小さいことである。これは式で書けば ui (s1, ・・・, si-1, si', si+1, ・・・, sn)　＜　ui (s1, ・・・, si-1, si'' , si+1, ・・・, sn) が他のプレーヤーの戦略集合 S1, ・・・, Si-1, Si+1, ・・・, Sn 　から選んだどの (s1, ・・・, si-1, si+1, ・・・, sn) についても成り立つということである。 　＜　はぁ〜、わかんないれす 　＜　むつかしいねぇ 　＜　n=2 のとき i=2 で考えましょう 「 G = {S1, S2 ; u1, u2} を考え、 s2' と s2'' をプレーヤー 2 のとりうる戦略であるとする（つまり s2' と s2'' はともに S2 の要素であるとする）。 このとき戦略 s2' が戦略 s2'' によって強く支配されるとは、1 のどんな戦略に対しても、 2 が s2' を選んだときの利得が s2'' を選んだときの利得より厳密に小さいことである。これは式で書けば u2 (s1, s2')　＜　u2 (s1, s2'') が 1 の戦略集合 S1 から選んだどの s1 についても成り立つということである。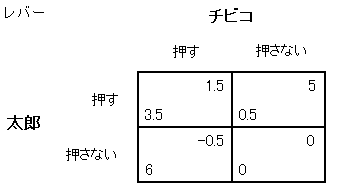」 合理的なハムスターを思い出してください。 このゲームではチビコの「押す」が支配される戦略でした。 このとき太郎のどんな戦略に対しても、チビコが「押す」 を選んだときの利得は「押さない」を選んだときの利得より厳密に小さいです。 これは式で書けば u2 (s1, 押す)　＜　u2 (s1, 押さない) が太郎の戦略集合 S1 から選んだどの s1 についても成り立つということです。じっさい u2 (押す, 押す)　＜　u2 (押す, 押さない) u2 (押さない, 押す)　＜　u2 (押さない, 押さない) です。 ◆参考文献 『経済学のためのゲーム理論入門』　 ロバート・ギボンズ、創文社、1995年 GAME THEORY FOR APPLIED ECONOMISTS (1992)