ナッシュ均衡（純粋戦略）

3. ナッシュ均衡（純粋戦略） 定義　 n 人の標準型ゲーム G = {S1, ・・・, Sn ; u1, ・・・, un} を考えたとき、 戦略 (s1*, ・・・, sn*) がナッシュ均衡であるとは、各プレーヤー i の戦略 si* が他の (n-1) 人のプレーヤーのとる戦略 (s1*, ・・・, si-1*, si+1*, ・・・, sn*) への最適反応となっていることである。式で書けば、 Si に属するどんな戦略 si に対しても ui (s1*, ・・・, si-1*, si*, si+1*, ・・・, sn*) ≧ ui (s1*, ・・・, si-1*, si , si+1*, ・・・, sn*) が成り立つこと、すなわち si* が max ui (s1*, ・・・, si-1*, si , si+1*, ・・・, sn*) , si∈Si の解となっていることである。 記号の意味 max f(x) の解　： 関数 f(x) の最大値を与える x , 最適解のこと。 a∈A　：　a は集合 A の要素である。 　＜　n=2 のとき i = 1, 2 で考えるのだぴょん 　　＜　ほーい 2 人の標準型ゲーム G = {S1, S2 ; u1, u2} を考えたとき、 戦略 (s1*, s2*) がナッシュ均衡であるとは、 まず、プレーヤー 1 の戦略 s1* がプレーヤー 2 のとる戦略 s2* への最適反応となっていることである。式で書けば、 S1 に属するどんな戦略 s1 に対しても　u1 (s1*, s2*) ≧ u1 (s1, s2*)　が成り立つこと、すなわち s1* が　max u1 (s1, s2*)　の解となっていることである。 そして、プレーヤー 2 の戦略 s2* がプレーヤー 1 のとる戦略 s1* への最適反応となっていることである。式で書けば、 S2 に属するどんな戦略 s2 に対しても　u2 (s1*, s2*) ≧ u2 (s1*, s2)　が成り立つこと、すなわち s2* が　max u2 (s1*, s2)　の解となっていることである。 (s1*, s2*) がナッシュ均衡であるとは、 s1* が max u1 (s1, s2*) の解であり、 s2* が max u2 (s1*, s2) の解であるということです。 具体的に考えてみましょう。合理的なハムスターを思い出してください。 このゲームでは (太郎, チビコ) = (押す, 押さない) がナッシュ均衡でした。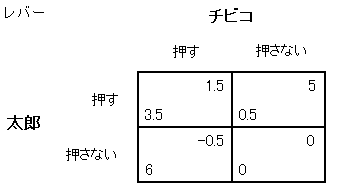 　 太郎の利得関数　u1 (s1, s2) 　は、 (押す, 押す) = 3.5 (押す, 押さない) = 0.5 (押さない, 押す) = 6 (押さない, 押さない) = 0 です。 太郎のとる戦略「押す」は、チビコのとる戦略「押さない」への最適反応になっています。 これは式で書くと、　(押す, 押さない) ≧ (押さない, 押さない)　が成り立つということです。 max u1 (s1, s2*) の解　というのは、高校の数学でいえば「この関数が最大値をとるときの x を求めよ（条件に注意して）」みたいなかんじです。《チビコの「押さない」 = s2* を前提としたとき、利得を最大にする戦略》ということです。これは「押す」です。 チビコについても同様に考えます。 チビコの「押さない」は　max u2 (s1*, s2) の解です。 ◆参考文献 『経済学のためのゲーム理論入門』　 ロバート・ギボンズ、創文社、1995年 GAME THEORY FOR APPLIED ECONOMISTS (1992)