|
5. 期待利得
- J で S1 に属する純粋戦略の数、
K で S2 に属する純粋戦略の数を示す。
S1 = { s11 ,・・・, s1J } ,
S2 = { s21 ,・・・, s2K }
として、
s1j , s2k でそれぞれ
S1 , S2 に属する任意の純粋戦略を指す。
- もしプレーヤー1が、プレーヤー2は戦略
(s21 ,・・・, s2K) を
確率 (p21 ,・・・, p2K) で選択すると予想すれば、
プレーヤー1が純粋戦略 s1j を選ぶことによって得る期待利得は

と書ける。
-
また、プレーヤー1が混合戦略 p1 = (p11 ,・・・, p1J ) を選べば、プレーヤー1の期待利得は
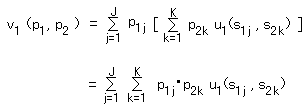
となる。
- 同様にして、
プレーヤー2の期待利得は

となる。
|
J=2, K=2 のときを考えます。
アイの戦略集合を S1 、ノノの戦略集合を S2 とします。
S1 = { s11 , s12 } ,
S2 = { s21 , s22 }
として、
s1j , s2k でそれぞれ
S1 , S2 に属する任意の純粋戦略を指します。
もしアイが、ノノは戦略
(s21 , s22) を
確率 (p21 , p22) で選択すると予想すれば、
アイが純粋戦略 s1j を選ぶことによって得る期待利得は
どうなるでしょう。
これは、たとえば j=1 のときは、
アイが s11 を選んだときの期待利得ということなので、
p21*8 + p22*0 になります。これは
p21 u1 (s11 , s21) + p22
u1 (s11 , s22)
ということです。
j=2 のときは、 s12 を選んだときの期待利得なので p21*0 + p22*6 です。
これは
p21 u1 (s12 , s21) + p22
u1 (s12 , s22)
です。
結局アイが s1j をとったときの期待利得は
p21 u1 (s1j , s21) + p22
u1 (s1j , s22)
で、これは
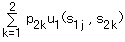
と書けます。
いま、アイが混合戦略 p1 = (p11 , p12 ) を選ぶとします。
するとアイの期待利得は
p11(s11をとったときの期待利得) + p12
(s12をとったときの期待利得) なので、
p11 (
p21 u1 (s11 , s21) + p22
u1 (s11 , s22) ) +
p12 (
p21 u1 (s12 , s21) + p22
u1 (s12 , s22) )
です。これは、
p11(p21*8 + p22*0)+
p12(p21*0 + p22*6)
=
p11p21*8 + p11p22*0 +
p12p21*0 + p12p22*6
のことで、結局アイが混合戦略 p1 、ノノが混合戦略 p2
をとったときのアイの期待利得は
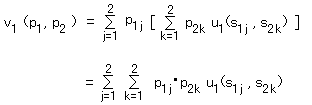
と書けます。式は (j, k) = (1, 1), (1, 2), (2, 1), (2, 2) で和をとるという意味です。
v1 (p1 , p2) =
p11 * p21 u1 (s11 , s21) +
p11 * p22 u1 (s11 , s22)
+
p12 * p21 u1 (s12 , s21)
+
p12 * p22 u1 (s12 , s22)
同様に考えてノノの期待利得は

で
v2 (p1 , p2) =
p11 * p21 u2 (s11 , s21) +
p11 * p22 u2 (s11 , s22)
+
p12 * p21 u2 (s12 , s21)
+
p12 * p22 u2 (s12 , s22)
です。
◆参考文献

|
 期待利得
期待利得
 期待利得
期待利得