Game Theory 101

　ナッシュ均衡（混合戦略）　

6. ナッシュ均衡（混合戦略）
定義　 2 人プレーヤーの標準型ゲーム G = {S₁, S₂ ; u₁, u₂} において、混合戦略 (p₁^*, p₂^*) がナッシュ均衡であるとは、各プレーヤーの混合戦略が他のプレーヤーの混合戦略に対する最適反応となっていること、つまり、
v₁ (p₁^*, p₂^*) ≧ v₁ (p₁, p₂^*)
v₂ (p₁^*, p₂^*) ≧ v₂ (p₁^*, p₂)
が成立することである。

＜　「あいとのぞみ」は混合戦略まで考えるともう１個ナッシュ均衡があるのだぴょん。
＜　まじでー、でじまー

アイ：　(パチンコ, 映画) = (2/3, 1/3)
ノノ：　(パチンコ, 映画) = (1/3, 2/3)
の混合戦略の組はナッシュ均衡であることがわかります。

アイの期待利得は
2pq+0(1-p)q+0p(1-q)+1(1-p)(1-q)
= 2pq+(1-q-p+pq)
= -p-q+3pq+1
= (-1+3q)p-q+1
ノノの期待利得は
1pq+0(1-p)q+0p(1-q)+2(1-p)(1-q)
= pq+2(1-q-p+pq)
= -2p-2q+3pq+2
= (-2+3p)q-2p+2
です。
アイは　q = 1/3 のときすべてのp が最適反応
ノノは　p = 2/3 のときすべてのq が最適反応
です。

p, q の組 (2/3, 1/3) ではお互いに最適反応しています。したがって　(p, q) = (2/3, 1/3)　はナッシュ均衡になります。このときの期待利得はともに 2/3 です。
　

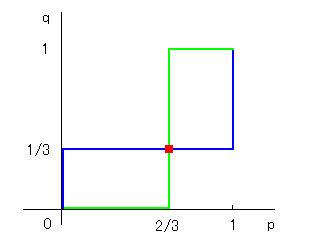
青色の線がアイの最適反応、緑色の線がノノの最適反応を表します。いま　(p, q) = (2/3, 1/3)　にいるとします。このときアイは自分だけ 2/3 から離れてみても期待利得を上げることはできません。同様にノノは自分だけ 1/3 から離れてみても期待利得を上げることはできません。これが

v₁ (p₁^*, p₂^*) ≧ v₁ (p₁, p₂^*)
v₂ (p₁^*, p₂^*) ≧ v₂ (p₁^*, p₂)

の意味です。
たとえば、 (p, q) = (1/2, 1/2) はナッシュ均衡になりません。アイは、ノノの q=1/2 を前提にしたとき、 p=1 にすることで利得を上げることができます。これは　v₁ (p₁^*, p₂^*) ≧ v₁ (p₁, p₂^*) 　が成り立っていないということです。

◆参考文献

『経済学のためのゲーム理論入門』　
ロバート・ギボンズ、創文社、1995年
GAME THEORY FOR APPLIED ECONOMISTS (1992)