破産する確率

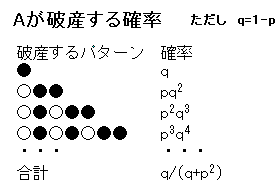
いま、あるゼロサムゲームを考えます。ＡがＢに勝つ確率を p とします。それぞれの所持金はＡが1(単位金)、Ｂは2(単位金)とします。1回の賭け金は1(単位金)です。 どちらかが破産したときゲームが終わりになるとすると、ＡとＢはどちらが有利でしょうか？なんとなくＢが有利そうですよね。だってＡは1回目に負ければそれで終わりなのに、 Ｂはまだ2回目があります。じつはこのゲームは「破産すると終わりになるゲームでは、資金が少ない方が不利になる」ということを示す確率モデルなのです。それでは実際に計算してみましょう。 破産するパターンで場合分けして、Ａが破産する確率は q+pq2+p2q3+p3q4+ ・・・　 これは公比 pq の無限等比級数です。 そして -1 < pq < 1 なので、収束します。 和は S= q/(1-pq) = q/(1-p(1-p)) = q/(1-p+p2) = q/(q+p2) よってＡが破産する確率は q+pq2+p2q3+p3q4+・・・＝q/(q+p2)　　　　(ただし q=1-p) 　　　・・・　※　　　　 です。 p=q=1/2 とします。つまりＡもＢも勝つ確率が同じとします。 このときＡが破産する確率は (1/2)/((1/2)+(1/4))=2/3 です。 Ａが少し不利で p= 2/5 とします。するとＡが破産する確率は (3/5)/((3/5)+(2/5)2)= 15/19 にもなってしまいます。 Ａが有利で p= 3/5 としても、 Ａが破産する確率は (2/5)/((2/5)+(3/5)2) = 10/19 で、 1/2 を少し上回るぐらいです。 ※ q+pq2+p2q3+p3q4+・・・＝q/(q+p2)　について これは高校の理系で習う「極限」の考え方ですので、すこし説明をしておきます。 q+pq2+p2q3+p3q4+・・・ 　のような式を無限級数といいます。この場合、もとの数列が等比数列なので、とくに無限等比級数といいます。無限等比級数はある実数Sに収束することがあります。 それはもとの等比数列の公比が -1 < r < 1 のときです。 1より小さい数をどんどん掛けていけば、無限にも終わりがありそうですよね。 この例では公比は pq で、0から1の間の数字です。 そこでこの無限級数は収束し、和をもつことになります。 もとの数列は 初項 q 、公比 pq の等比数列です。一般項は an=q(pq)n-1 です。 この数列の第n項までの和は、 等比数列の和の公式 Sn= a(1-rn) / (1-r)　　（a は初項、r は公比）　により Sn= q｛1-(pq)n｝ / (1-pq)　　 です。無限級数は、「等比数列の第n項までの和」におけるnを無限に大きくするということです。 Snのnを無限に大きくするということです。ここで (pq)n に注目してください。 pq は0から1の間の数字です。そういう数字をどんどん掛けていくと、最後には0になりますよね。これは nを無限に大きくすると、(pq)nは0になるということです。 するとSnは q(1-0) / (1-pq)　になります。すなわち Snは q / (1-pq)　になります。あとは上と同じです。 無限等比級数 収束条件 -1 < r < 1 和は　S = a / (1-r)　 ◆参考文献 鈴木義一郎『確率でみる人生』