娘。の組合せ
|
今回は確率論の基本の基本である「順列と組み合せ」です。
さて、そもそも確率の定義というのは 
ということです。なので本来、「個数の処理」というのが確率論の基本にあるわけです。 そして、個数の処理を簡単にするために使うのが 「！」とか「Ｐ」とか「Ｃ」という記号です。 ◆まず「！」。エクスクラメーションマーク（exclamation mark）です。 １からｎまでの正の整数の積を n の階乗といい、n！で表します。 たとえば「タンポポの４人のメンバーの並び方」を考えてみましょう。 「乙女、パスタに感動」では通常、左から石川、加護、矢口、飯田と並ぶことになっていますが、 並び方はいろいろあります。     これは 「積の法則」により「４×３×２×１＝２４通り」です。 そしてこれをスマートに書きたいので、「！」を使って、「４！通り」とします。 
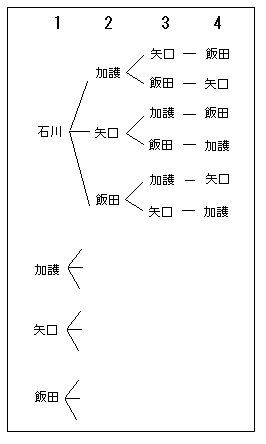
積の法則とは 「Ａとなる場合が a 通り、Ｂとなる場合が b 通りあるとき、 ＡにつづいてＢとなる場合の数は a×b 通り」というものです。 よって「１が４通り、つづく２が３通り、つづく３が２通り、つづく４が１通り」 と考え４×３×２×１＝２４通りということです。 （左から４本の枝が３倍、２倍、１倍に分裂していく。）
◆次に「Ｐ」。これは permutation のＰで、順列を表す記号です。
「ｎ個のものからｒ個とって左右に１列に並べる」といったとき、
このように並べたものを「異なるｎ個のものからｒ個とった順列」といいます。 「モーニング娘１０人から、３人をとって、左から１列に並べる」というのを考えるときがこれです。積の法則により、 いちばん左が１０通り、つぎが９通り、つぎが８通りと考え １０×９×８＝７２０通りです。 これをスマートに書くとき、「10Ｐ3通り」とします。
◆そして「Ｃ」。combination のＣで、組み合せを表す記号です。
「ｎ個のものからｒ個とった組」を、「ｎ個のものからｒ個とる組み合せ」といい、 「モーニング娘１０人から３人組の新ユニットをつくろう」というときがこれです。 組み合せは10Ｃ3通りです。 そして 10Ｃ3＝10Ｐ3 / 3 ! になります。これはつぎのようにしてわかります。 10人から3人をとる順列の総数は10Ｐ3です。 これを「まず10人から3人取り出すことを考え→次にその3人を並べかえる」 と考えます。第1段階の「10人から3人を取り出す取り出しかた」を x とします。 次の「取り出した3人の並べ方」は 3 ! 通りです。 よって合わせて x × (3 !) 。 10Ｐ3＝x × (3 !) となり、 x ＝10Ｐ3 / 3 ! です。 10Ｃ3 ＝10Ｐ3 / 3 ! ＝ 720/6 ＝ 120 いろいろ考えてみると楽しいです。
★ロト６ 2000年10月 先日、新しい宝くじ「ロト６」が発売されました。 １から４３までの数字の中から異なる６つの数字を選び、抽選した数字といくつ一致したかで１等から５等までの順位が決定します。１口は200円。 第１回の抽選で選ばれた数字は「03, 08, 10, 13, 27, 30」で、１等は約4500万円だったそうです。 「１から４３までの数字の中から異なる６つの数字を選ぶ」選び方は
N ＝43Ｃ6
１等はそのうちの a=1 （通り）。６つの数字がすべて一致する場合です。 確率の定義
に従い、１口買った場合、１等が当たる確率 P(A)は P(A) = a/N = 1 / 6096454 です。 第１回の発売では約11億8000万円が売れたそうです。 口数にすると、1,180,000,000 / 200 = 5,900,000 口。 ということは、すべてばらばらのものが買われたとしても、 6,096,454 （通り）に届かなかったわけです。 あまりにも組み合せ数が多いので、当選者がいないということもありえます。 そこで、当選者がいない順位の賞金は次回の1等賞に繰り越す「キャリーオーバー」 が初めて採用されています。 ★３連複馬券 2000年11月 先日（2000/11/16）、JRAが2002年からの馬単および3連複馬券の導入を発表しました。 18頭立ての場合、3連複は 18Ｃ3 = (18*17*16)/(3*2*1) = 816 通り です。 馬連（153通り）の約5.3倍当たりにくくなります。よって平均配当も馬連の5.3倍になります。 馬連の平均配当がだいたい5000円弱ということなので、25000円ぐらいですか。 うーん、すごいですね。 でも流しで買うとすると13600円（17Ｃ2通り）かかる計算になりますね・・・。
◆組合せの公式はつぎのような形にするとおぼえやすいです。
たとえば 10P3 = 10*9*8 = 10*9*8*7*6*5*4*3*2*1 / 7*6*5*4*3*2*1 = 10!/ 7! とかけるので 10C3 = 10P3 / 3! = (10!/ 7!) / 3! = 10! / 7!3! です。 一般的には
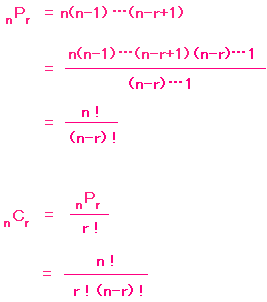
となります。
|
