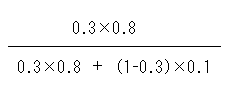ベイズの定理

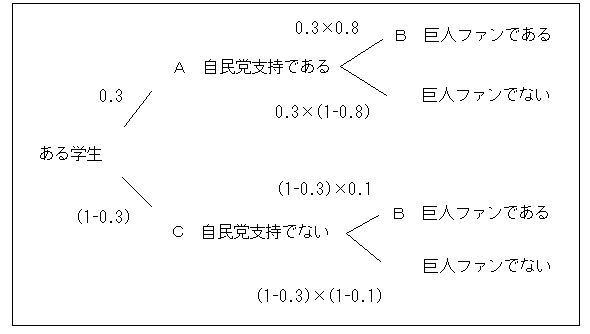
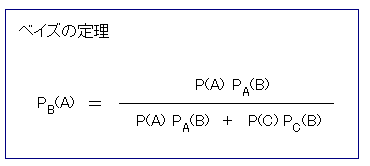
ある革新系の大新聞が都内の大学生1000人に対しアンケート調査をした。 質問項目は２つ。Q1.「あなたは自民党を支持しますか？」、Q2.「あなたは巨人ファンですか？」。調査の結果、自民党支持者のうち、80％が巨人ファンであることがわかった。また、自民党を支持しない人のうち、10%が巨人ファンであるということがわかった。 学生のうち、自民党支持者は30％だった。無作為に選んだ学生が、巨人ファンだったとき、その学生が自民党支持者である確率はいくらか。 こういう問題を解くときは「ベイズの定理」というのを使います。 Ａ：自民党支持 Ｂ：巨人ファン Ｃ：自民党不支持 とします。ＣはＡの余事象です。 PA(B) = 0.8, PC(B) = 0.1, P(A) = 0.3, P(C) = 0.7 より、 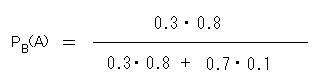PB(A) = 0.24 / (0.24 + 0.07) = 0.24 / 0.31 = 0.774　・・・(答) ◆ベイズの定理の証明 事象Ａの余事象Ｃを利用して、＜条件ＢつきのＡの確率＞を求めます。 ベイズの定理は図にすると簡単です。 図よりただちに「巨人ファンだったとき自民党支持者である確率」が求まります。すなわち、＜「自民党支持者で巨人ファン」または「自民党支持者でなくて巨人ファン」＞のうち、＜「自民党支持者で巨人ファン」＞の割合なので