条件つき確率

今回は「条件つき確率」です。次の「ベイズの定理」のステップになります。 いま、52枚のカードから2枚続けて引くことを考えます。このとき、以下の問題を考えてみてください。 問題1　少なくとも1枚キング（K）を引く確率はいくらでしょうか。 問題2　少なくとも1枚クイーン（Q）を引く確率はいくらでしょうか。 答え　まず、52枚のカードから2枚を取り出す方法は 52C2 = 52*51/2*1 = 1326 通り。そのうちキングを1枚も含まないケース（余事象）を考えます。これはキングを除く48枚のカードから2枚を取り出す方法の数だから、 48C2 = 48*47/2*1 = 1128 通り。したがって少なくともキングを1枚含むのは 1326-1128 = 198 通り。求める確率は 198/1326 = 0.149 。問題2も同様に考えて 198/1326 = 0.149 。 P(K) = 198/1326 , P(Q) = 198/1326 . 問題3　キング（K）とクイーン（Q）の両方を引く確率はいくらでしょうか。 答え　キングとクイーンの組み合わせは全部で 4*4 = 16 通りあります。したがって求める確率は 16/1326 = 0.012 。 P(KQ) = 16/1326 . さて、問題はここからです。 問題4　ある人がこのゲームを1プレイだけしました。すると2枚のうち1枚はクイーン（Q）でした。このとき、もう1枚がキング（K）である確率はいくらでしょうか。 答え　これは、相手の手札が運良く1枚だけ見えてしまったときに、もう1枚が何であるかを予想するというシチュエーションです。 いま、何も情報がないときには、 相手がキングをもっている確率は 0.149 と考えます。そこで問題は、2枚の手札のうち1枚がクイーンであることが明らかになったときに、どう考えるかということです。 むずかしいですね。これはつぎのように考えます。まず、相手の手札の1枚がクイーンであるとき、相手の手札は198通りのうちのいずれかであることがわかります。 （クイーンを含まないケースが1128通りあって、クイーンを含むケースが198通りあることはすでに見ました。） そこでいま関心があるのは、このクイーンを含むペアの中にキングが含まれているかどうかということです。 ところがこれはいいかえれば、 キングとクイーンのペアになっているかどうかということです。 これは問題3で見たように16通りです。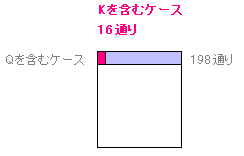 クイーン（Q）を含むという情報を得たことで、 いまや考えるべき標本空間は、 クイーンを含むケース（198通り）にしぼられたのです。 そしてクイーンを含むケース（198通り）を新しく「全体」と考えたとき、 そのうちキングをも含むケース（16通り）にだけ関心があるので、 求める確率は 16/198 = 0.081 になります。 これは条件つき確率とよばれます。 条件「Qを含む」つきの「Kを含む」確率ということで、 PQ(K) とか P(K|Q) で表記します。 P(K|Q) = 16/198 ところで、 P(K|Q) = 16/198 の分子・分母をもともとの全体の場合の数1326で割ると P(K|Q) = (16/1326)/(198/1326) となって、 P(K|Q) = P(KQ)/P(Q) であることがわかります。 問題5　キング（K）またはクイーン（Q）を引く確率はいくらでしょうか。 答え　キングかクイーンを含んでいればよいということです。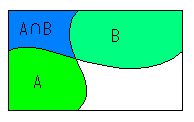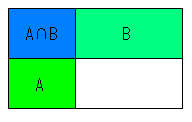 図で和集合の大きさを考えます。 一般に n(A∪B) = n(A) + n(B) - n(A∩B) なので、考えている和集合の大きさは 198+198-16 = 380 になります。 求める確率は 380/1326 = 0.287 （別解）やはり余事象を考えます。キングとクイーンを除く44枚から2枚を取り出す方法は 44C2 = 44*43/2*1 = 946 通り。考えている場合の数は 1326 - 946 = 380 通り。求める確率は 380/1326 = 0.287 ◆条件つき確率 １つの試行Ｔの全事象をＵ、ＡとＢを２つの事象とする。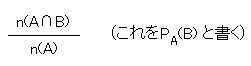 このとき は、事象Ａの中だけで考えたとき、その中でＢに属する根元事象(*)の起こる割合を表している。この値を条件ＡのもとでのＢの確率、あるいは条件ＡつきのＢの確率 という。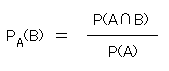分子・分母を n(U) で割り、 (*)根元事象 １つの試行Ｔで、起こりうるすべての場合の集合Ｕを、その試行の標本空間といい、この集合の要素を根元事象という。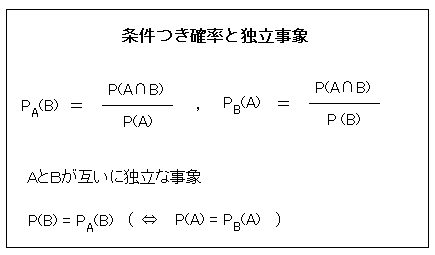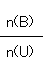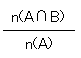 ◆独立事象 一般に PA(B) = P(B) ではないが、Ｕ全体の中でＢの占める割合 が、Ａの中だけでＢの占める割合 に等しいことがある。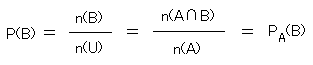これは となることである。 次の裏づけもあって、ＡとＢは互いに独立な事象であるという。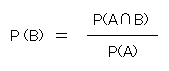 ◆P(B) = PA(B) ならば P(A) = PB(A) ＜証明＞ P(B) = PA(B) とは ということ。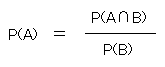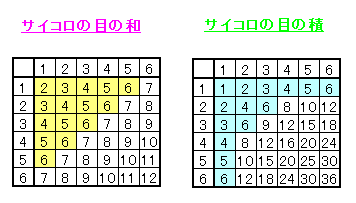このとき であるから P(A) = PB(A) 積の法則 ＡかつＢである確率 P(A∩B) ＝ P(A) PA(B) ＝ P(B) PB(A) 2個のサイコロを同時に投げたとき、2つの目の和が6以下である事象をA、2つの目の積が6以下である事象をBとする。このとき (1) A、Bは独立な事象か？ (2) PB(A) を求めよ。 (1) A、Bは独立な事象か？ サイコロの目の、「A：和が6以下であること」と「B：積が6以下であること」は、関係があるのかということです。 関係がある、すなわち独立でないことを示すには、 PA(B) ≠ P(B) を証明すればよいです。 図のように、サイコロの目の和が6以下になるのは (1, 1) , (1, 2) , (1, 3) , (1, 4) , (1, 5) , (2, 1) , (2, 2) , (2, 3) , (2, 4) , (3, 1) , (3, 2) , (3, 3) , (4, 1) , (4, 2) , (5, 1) の 15 通り。 よって P(A) = 15/36 = 5/12 また、サイコロの目の積が6以下になるのは (1, 1) , (1, 2) , (1, 3) , (1, 4) , (1, 5) , (1, 6) , (2, 1) , (2, 2) , (2, 3) , (3, 1) , (3, 2) , (4, 1) , (5, 1) , (6, 1) の 14 通り。 よって P(B) = 14/36 = 7/18 サイコロの目の和が6以下という条件のもとで、目の積が6以下になるのは (1, 1) , (1, 2) , (1, 3) , (1, 4) , (1, 5) , (2, 1) , (2, 2) , (2, 3) , (3, 1) , (3, 2) , (4, 1) , (5, 1) の 12 通り。 よって PA(B) = 12/15 = 4/5 ≠ P(B) (2) PB(A) を求めよ。 積の法則　 P(A) PA(B) ＝ P(B) PB(A) 　より PB(A) ＝ {P(A) PA(B)} / P(B) ＝ (5/12)(4/5)(18/7) ＝ 6/7