確率の定義

いま、１から３までの数字を書いたカードが１枚ずつ計３枚あるとします。 カードを裏返しにしてよくかきまぜた後、３枚のカードをふせたまま左から順に テーブルの上におきます。そこで、カードを開けたとき、カードの数字が、左から右へ、小さいものから大きいものへと順に並んでいる確率を求めましょう。 これは順列を考えればよいのですね。 並び方は３！通りです。そしてそのうち条件をみたすような並び方は （1 - 2 - 3）だけです。よって求める確率は 1/ 3! となります。 ▼ 問題をすこしむずかしくしてみましょう。 いま、52枚のトランプからハートだけ13枚抜き取ります。 これらを同様に裏返しにしてまぜた後、任意に ――― えっと「任意に」というのは「どれでも」という意味です ――― ３枚をとり、カードをふせたまま左から順に テーブルの上におきます。そこで、カードを開けたとき、カードの数字が、左から右へ、小さいものから大きいものへと順に並んでいる確率を求めましょう。 エースは１と数え、ＪＱＫが１１〜１３です。 同じく順列を考えます。 並び方は 13P3 通りですね。そして、このうち小さい順に並ぶのは何通りかということです。 を思い出してください。 順列の総数を「３枚とりだして→それらを並べる」と考えたんでしたよね。 13P3 ＝ 13C3 ×３！ 小さい順に並ぶのは、１つの組み合せに対して、１通りに決まります。 だから、13P3 のうち、 小さい順に並ぶのは、最初に取り出した組み合せの数だけあるのです。 よって求める確率は 13C3 / 13P3 = 1/ 3! になります。 あれ、これはカードが３枚のときと同じですよね？カードが３枚から１３枚に増えても、確率は同じ 1/ 3! 。なんとなく不思議ですよね。じつはこれはカードが何枚に増えても同じなのです。 ▼ いま、１から n ( n ≧ 3 )までの数字を書いたカードが１枚ずつ n 枚あるとします。 カードを裏返しにしてよくかきまぜた後、３枚のカードをふせたまま左から順に テーブルの上におきます。そこで、カードを開けたとき、カードの数字が、左から右へ、小さいものから大きいものへと順に並んでいる確率を求めます。 同様に考えて、並び方は nP3 通り。 そのうち小さい順に並ぶのは nC3 通り。 よって求める確率は nC3 / nP3 ところが、 nＣr＝nＰr / r ! に注意して、 nＣ3＝nＰ3 / 3 ! よって　 nC3 / nP3 = 1/ 3! ◆試行 サイコロを投げたり、トランプを並べたりすることを試行といい、Ｔで表す。 ◆事象 １つの試行Ｔで、起こりうるすべての場合の集合Ｕを、その試行の標本空間といい、 この集合の要素を根元事象という。 とくに標本空間自体のことを全事象という。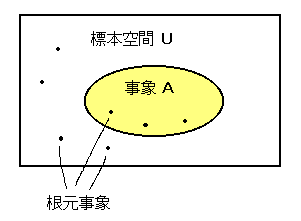 ◆事象の確率 根元事象 u には、その起こる割合が考えられる。 それを P(u) で表し、 u の起こる確率という。 Ａ＝｛u1, ……, ur｝を事象とするとき、Ａの要素 ui の確率の和 P(u1)＋・・・＋P(ur) ＝ P(A) を、事象Ａの起こる確率という。 とくに P(U)＝（Ｕのすべての要素の確率の和）＝１ ◆確率の定義 とくに各根元事象 u の起こる割合が等しいと考えられる場合は、根元事象は 「同様に確からしい」といわれる。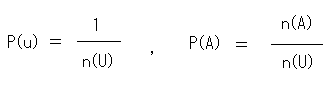このときは、全根元事象の総数、すなわち集合Ｕの大きさを n(U) とし、事象Ａに属する根元事象の総数を n(A) とすると これが確率の定義である。