 祭の作り方 |
 |
|
20人のメンバーをシャッフルして3つのユニットを作る方法は、
じつに 580,606,446 通りもあります。
仮に投票で決めるとして、もし全く同じ方法を考えた人がいたとしたら、それはきっと運命の人でしょう。5億8千・・・ほんとにそんなにあるんでしょうかね。
これは20個の異なるものの集合を、3つの部分集合に分割する方法です。（ただし部分集合に空集合があってはならないとします。）今回はこれの計算の仕方を考えてみます。
まず手始めにつぎの問題を考えてみてください。 問題1 プッチモニの3人がホテルに泊まります。3人を2つの部屋（エレベーターに近いほうと遠いほう）に分配する方法はいくつあるでしょうか。ただし空の部屋はないとします。
まずつぎのように考えてみます。すなわち「ごっちんをどっちの部屋に→よっすぃーをどっちの部屋に→やっすーをどっちの部屋に」と考えて 2*2*2 = 8 通り。 ところが、これでは3人とも同じ部屋に入ってしまう場合も含まれてしまいます。 このような場合は2通りあります。そこで求める場合の数は 8-2=6 通りになります。 これを f (3, 2) = 6 と書くことにしましょう。ただし f (n, k) ： 異なる n 人のメンバーを異なる k 個の部屋に分配する方法 です。 これをもとにつぎの問題を考えてみてください。 問題2 n 人の娘。がホテルに泊まります（ただし n≧2）。 n 人を2つの部屋（エレベーターに近いほうと遠いほう）に分配する方法はいくつあるでしょうか。ただし空の部屋はないとします。 これはまず「1人目をどっちの部屋に→2人目をどっちの部屋に→・・・」と考えて 2n 通り。 n人すべてが同じ部屋に入ってしまう場合を除いて 2n -2 通り。 f (n, 2) = 2n -2 問題3 6人の娘。がホテルに泊まります。 6人を異なる3つの部屋に 分配する方法はいくつあるでしょうか。ただし空の部屋はないとします。 3つの部屋を R1, R2, R3 とします。 まず、空の部屋があってもよいとすると 36=729 通り。 ここからいずれかが空になるケースを除きます。 これは図にかくと斜線の部分になります。
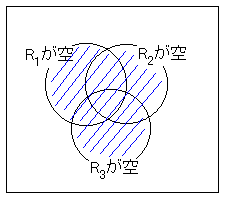
これはとりあえずつぎの公式を使って求めます。 m(A∪B∪C) = m(A) + m(B) + m(C) - m(A∩B) - m(B∩C) - m(C∩A) + m(A∩B∩C) R1 が空になる場合。 これは 6 人を異なる2つの部屋に分ける場合の数と同じなので 26=64 通り。 同様にして R2 が空になる場合も 26=64 通り、 R3 が空になる場合も 26=64 通り。 そして
R1と R2が空になる場合。1通り。 そして すべての部屋を空にすることはできないです。 以上より 64 + 64 + 64 - 1 - 1 - 1 + 0 = 189 これがいずれかが空になる場合の数です。
したがって求める場合の数は 729-189=540 通り。 問題4 n 人の娘。がホテルに泊まります（ただし n≧4）。 n 人を異なる3つの部屋に分配する方法はいくつあるでしょうか。ただし空の部屋はないとします。 問題3をもとに考えます。 まず、空の部屋があってもよいとすると 3n 通り。 ここからいずれかが空になるケースを除きます。 これが 2n + 2n + 2n - 1 - 1 - 1 + 0 通り。
したがって求める場合の数は f (n, 3) = 3n - ( 3*2n - 3 ) = 3n - 3*2n + 3
問題5 20人のハロプロメンバーがホテルに泊まります。20人を3つの部屋に分配する方法はいくつあるでしょうか。ただし部屋には区別をつけないとします。また空の部屋はないとします。 20人を区別のある3つの部屋に分ける方法は f (20, 3) 通り。 ここでは部屋の区別をなくせばよいので、「束ね」の考えより 求める場合の数は
f (20, 3) / 3!
|
後藤 
吉澤 
保田