 娘。の振り分け |
 |
|
問題1 某テレビ番組の海外ロケ企画。
モーニング娘。の9人がハワイ、台湾、オーストラリアへ行くことになりました。
3つのロケ地には3人ずつ振り分けることになっています。
このとき、振り分ける方法はいくつあるでしょうか。
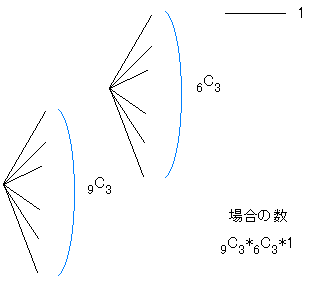
これはつぎのように流れ作業で考えます。 「まずどの3人をハワイへ送るか→残った6人のうちどの3人を台湾へ送るか→残った3人は自動的にオーストラリア」。したがって 9C3*6C3 = 1680 通り。
問題2 モーニング娘。こんどは別のテレビ番組でゲームをやることになりました。 このゲームでは9人を3人ずつ3つのグループに分けなければなりません。 この方法はいくつあるでしょうか。
これはつぎのような流れ作業で考えます。 1の方法は、飯田を除く8人のうちどの2人を飯田と同じグループに入れるかということなので、 8C2 通り。 2の方法は、「6人のうちの年長者」の属するグループをつくる方法と同じです。 年長者を除く5人のうちどの2人を年長者と同じグループに入れるかということなので、 5C2 通り。 したがって 8C2*5C2 = 280 通り。
◆いま問題1を2段階に分けて考えます。つまり
第1段階： まず3つのチームに分ける ここで第1段階の場合の数を X 通りとします。 第2段階の場合の数は、3チームを並べる順列なので、 3!=6 通りです。 こうして求める場合の数は X*6 通りになります。
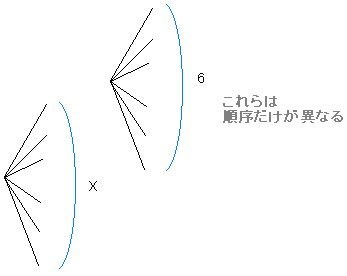
いっぽう、最初の方法で出した答えは1680通り。そこで X*6 = 1680 これを解くと X = 280 になります。これは第1段階の場合の数で、そして問題2で求める場合の数です。 そこで問題2の考え方として、 問題1で求めた場合の数を6で割るという方法があります。 1680/6 = 280 ◆ところでこれは、問題1でチームは同じで行き先だけ異なるものを6つずつ「束ねる」ようなものです。 たとえば次のような6通りのケースを考えましょう。
として
ハワイ−台湾−オーストラリア
という場合です。これらはどういう場合かというと、チームは同じで行き先だけ異なる ケースです。 (A, B, C), (D, E, F), (G, H, I) の3チームを1列に並べる順列なので 3!=6 通りあります。そして1680通りのうち6通りずつこういうものがあるので、 1860個を6個ずつ「束ねて」280個にすると考えます。
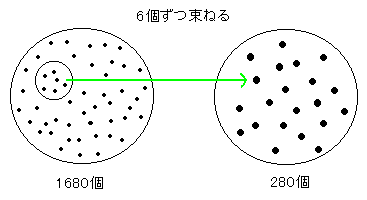
◆このような「束ね」の考えで
も同じように考えることができます。 異なる n 個から r 個とって1列に並べる方法が nPr 通りあって、 そのうち順序だけ異なるものが r! 個ずつあると考えます。 したがって異なる n 個から r 個とる方法は、 nPr を r! 個ずつ束ねて、 nPr/r! 通りです。 たとえば 異なる4個から2個とって1列に並べる方法は 4P2 通りあります。
a-b, a-c, a-d, このうち 順序だけ異なるものが 2! 個ずつあります。 したがって異なる4個から2個とる方法は、 4P2 を 2! 個ずつ束ねて、 4P2 / 2! 通りです。
◆このへんの考え方がわかりにくい場合は、競馬などでいう単式・複式を考えるとよいかもしれません。中央競馬では来年2002年から馬単が始まりますが、18頭立ての場合、 馬連は 18C2 = 153 通り。馬単は 18P2 = 306 通り。ちょうど2倍だけあります。 3連複は 18C3 = 816 通り。3連単は 18P3 = 4896 通り。ちょうど6倍だけあります。＜並び替えの分＞倍にするのです。束ねるというのはこれと逆の操作なので＜並び替えの分＞だけ割るのです。
問題3 8人を4人ずつ2つのチームに分ける方法はいくつあるでしょうか。 いまA組、B組に分ける方法は 8C4 * 4C4 = (8*7*6*5/4*3*2*1) * 1 = 70 通り。組の区別をしない場合はこれを 2! = 2 で割って、35通り。
問題4 8人を2人ずつ4つのチームに分ける方法はいくつあるでしょうか。
いまA組、B組、C組、D組に分ける方法は 8C2 * 6C2 * 4C2 * 2C2 = 28 * 15 * 6 * 1 = 2520 通り。組の区別をしない場合はこれを 4! = 24 で割って、105通り。
|
A 
B 
C
D 
E 
F
G 
H 
I