 ポーカー |
 |
|
いま交換なしのポーカーを考えます。52枚から5枚を取り出す組合せの総数は
52C5 です。 この中には R.S.F. からワンペアまで含まれているわけですが、今回はそれらの場合の数をすべて計算してみます。 ロイヤル・ストレート・フラッシュ これは簡単です。スペード、ハート、ダイヤ、クラブの各スートにつき ただ1通りですから合わせて4通りです。 ストレート・フラッシュ たとえばスペードのストレート・フラッシュは9通りあります。ストレートは A, 2, 3, 4, 5, 6, 7, 8, 9 のいずれかから始まるものです。 他のスートも同様に考えて合計36通りあります。 フォー・カード どの数字が4枚になるか。これは13通り。 それぞれの場合で残りの1枚は何でもよいです。 たとえばエースのフォーカードの場合は、残りの48枚から1枚とってくるので48通り。他の12通りのフォーカードについても同様に考えます。 したがって合計 13*48 = 624 通りです。 フル・ハウス これはちょっとやっかいです。いま適当にフルハウスを作ってみました。
3枚のやつを7、2枚のやつをJとしたわけですが、 これを「まず何を3枚にするか→つぎに何を2枚にするか」という流れ作業で考えると、この方法は 13*12=156 通りあるわけです。「8とQ」とか、「6と10」とか、全部で156通りです。 ところがこの7とJからなるフルハウスは他にも作れます。 これは「4種類の7のうちどの3つを選ぶか→4種類のJのうちどの2つを選ぶか」と考えて 4C3*4C2 = 4*6 = 24 通りの方法があります。「8とQ」とか「6と10」についても同様に24通りあります。 そこで156通りのそれぞれに対し24通りずつあるので、全部で 156*24 = 3744 通り。 これが求める場合の数です。
フラッシュ スペードのフラッシュは全部で 13C5 = 13*12*11*10*9 / 5*4*3*2*1 = 1287 通りです。 ところがこのうち、 R.S.F. とストレート・フラッシュとなるものは除かないといけません。スペードの R.S.F. は1通り、ストレート・フラッシュは9通りなので、 1287 - 10 = 1277 通りです。他のスートも同様に考えて合計 1277*4 = 5108 通りです。
ストレート
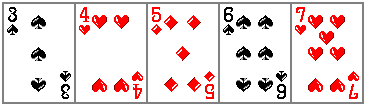
いま、3から始まるストレートというのはいくつ作れるでしょう。 これは「まず3のスートを決める→つぎに4のスートを決める→・・・→最後に7のスートを決める」と考えて 4*4*4*4*4 = 1024 通りです。 ただこのうちストレート・フラッシュになるケースが4通りあるので、これを除くと 1020 通りです。 他の A, 2, 4, 5, 6, 7, 8, 9, 10 についても同様に考えて、全部で 1020*10 = 10,200 通り。これが求める場合の数です。 スリー・カード
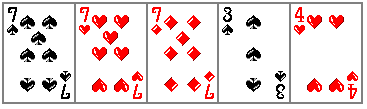
まず何を3枚にするかというのが13通りあります。 そしてそれぞれの場合について、 4つのスートのうちどの3つを使うか というのを考えます。これが 4C3 = 4*3*2 / 3*2*1 = 4 通り。 よってスリーカードの部分については計 13*4 = 52 通り考えられます。 ところが、残りの2枚の選び方が少しやっかいで、上の場合では7ではダメで、さらに 残りの2枚が同じ数字というのもいけません。 前者はフォーカード、後者はフルハウスになってしまうからです。 そこで残りの2枚についてはつぎのように考えます。 たとえば7のスリーカードの場合。 まず、7を除く12種類の数字から、どの2種類を使うかということを考えます。 これは 12C2 = 12*11 / 2*1 = 66 通りあります。 (5, 6) とか (8, 9) とか66通りです。 そしてそれぞれの場合のスートを考えます。 たとえば (5, 6) なら、「まず5のスートを何にするか→つぎに6のスートを何にするか」 と考えて 4*4 = 16 通りです。したがって合計 66*16 = 1056 通り。
3枚の部分が52 通り、 2枚の部分が1056通りなので、 全部で 52*1056 = 54,912 通り。これが求める場合の数です。 ツー・ペア
まず13種類のうちどの2つを使うかということで 13C2 = 13*12 / 2*1 = 78 通り。(A, J) とか (A, K) とか78通りです。 いま (A, J) を選んだ場合を考えましょう。 すると2枚のエースをどのスートにするかということで 4C2 = 4*3 / 2*1 = 6 通り。また2枚のジャックをどのスートにするかということで 4C2 = 4*3 / 2*1 = 6 通り。 したがってツーペアの部分は合計 78*6*6 = 2808 通りできます。 残りの1枚はツーペアに使わなかった11種類からどれを選ぶかということで11通り。 その1枚をどのスートにするかということで4通り。 したがって残りの部分の選び方は44通りです。 ツーペアの部分が2808 通り。 残りの部分が44通り。 全部で 2808*44 = 123,552 通り。これが求める場合の数です。 ワン・ペア
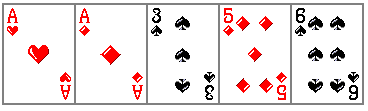
まず13種類のうちどれをペアにするかで13通り。 そして2枚をどのスートにするかということで 4C2 = 4*3 / 2*1 = 6 通り。 したがってワンペアの部分は全部で 13*6 = 78 通り。 残りの3枚は、残る12種類のうちどの3種類を使うかということで 12C3 = 12*11*10 / 3*2*1 = 220 通り。 たとえば (3, 5, 6) を使うとすると、それぞれのスートを決める方法が 4*4*4 = 64 通り。 したがって残りの3枚の部分は全部で 220*64 = 14080 通り。 ワンペアの部分が78通り。 残りの部分が14080通り。 全部で 78*514080 = 1,098,240 通り。これが求める場合の数です。 バースト 役がない場合は、すべての場合の数から、役がある場合を引いて
2598960 - (4+36+624+3744+5108+10200+54912+123552+1098240) です。 これですべての場合の数を数え上げました。 最後に 確率を計算したものが下の表です。何かの役がつく確率がちょうど 1/2 なんですね。
|
