アクセルロッドの実験
アクセルロッドの実験
|
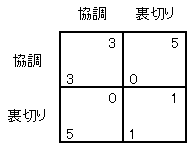
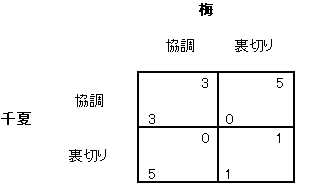
「繰り返し型囚人のジレンマ」はゲームとして遊べます。 クラスの黒板とか、職場のホワイトボードを使えば簡単です。 ここではショムニのホワイトボードを使い、例の6人にやってもらうことにしましょう。 まず、下の表のような囚人のジレンマを用意します。
これにしたがって得点を決めます。 試合を行なう2人はホワイトボードの両端に立ちます。 2人は同時に、協調なら ⊂ ( cooperation の C) を、 裏切りなら反対向きの ⊃ を書きます。
これを繰り返しやり、得点を競います。 ここでは1セット10回を1試合とし、6人のメンバーによる総当たり戦で行ないます。
ゲームはたとえばこんな感じです。 まず千夏と梅が対戦するとします。 千夏がいきなり裏切ってくるとします。そしてやはり梅も裏切るとします。 すると2人の得点は (千夏, 梅)=(1, 1) になります。 2回目は千夏が裏切り、梅は協調とします。すると (千夏, 梅)=(5, 0) です。 3回目は千夏が協調、梅も協調とします。すると (千夏, 梅)=(3, 3) です。 ここまでの合計得点は (千夏, 梅)=(9, 4) です。このようにして全部で10回やります。10回1セットを1試合とし、各人は5試合やるわけですが、 勝負は5試合の総得点です。 これが最も高かった人が優勝です。(1試合の平均得点を比べても同じです)。井上課長に飲みに連れていってもらえます。 このゲームにはいろんな戦略が考えられます。 もっとも単純なものとしてはつぎの3つが考えられます。
常に裏切る
常に協調する
ランダム化(裏切りと協調を50%ずつ) この他にもいろいろな戦略が考えられます。 最高得点が5、最低得点が0なので、毎試合の得点は 0〜50 の範囲になります。 どうですか、なかなか楽しそうでしょう?どうやったら総当たり戦の総合得点でトップになることができるのでしょうか。じつはこのゲームをコンピュータにやらせ、「おうむ返し」が最高の戦略であることを証明したのがアクセルロッドなのです。これはゲーム理論における重大な発見の1つとして位置付けられています。
アクセルロッドの実験は1セット200回で行ないます。 最高得点が5、最低得点が0なので、毎試合の得点は 0〜1000 の範囲になります。 第1回目の実験には、心理学や政治学、社会学などいろいろな分野から14の戦略が集まりました。プログラムには手の込んだものもたくさんありました。 しかし最高得点をあげたのは「おうむ返し」戦略で、その平均得点は504.5点でした。これはすでに説明したように「最初は協調から始め、あとは相手の前の手をまねる」という非常に簡単なものです。「おうむ返し」のような、上品でかつ、ときには制裁もくわえるという戦略は他にもいくつかあり、その点ではあまり驚きはありませんでした。しかしいちばん驚いたのは「おうむ返し」があまりにも簡単だということです。「おうむ返し」はさらに「自分の戦略を相手に知られてもかまわない」という重要な性質をもっています。さらにアクセルロッドが驚いたのは、「おうむ返し」は1試合1試合で見ると勝てなかったが、総合得点ではトップだった、ということです。 第2回目の実験には6か国から62の戦略が集まりました。たしかに第1回目は14の戦略しかなかったので、あらゆる戦略を網羅しているとはいえませんでした。 第2回目の実験の隠された狙いはもちろん「おうむ返し」を倒すことでした。 しかしまたしても勝ったのは「おうむ返し」でした。これで「おうむ返し」戦略は、幅広い戦略を相手にしても、勝つための最適条件を備えているということが、ほぼはっきりと証明されたのです。
◆参考文献
関連サイト
★ Department of Political Science, University of Michigan
★ Robert Axelrod
★ Serendip

|