タンポポアイランド
モームス市にはタンポポアイランドという人工島があります。
島から市の中心部に行くには2通りの方法があります。
1つは、モームス大橋を車で渡る方法、もう1つは海底鉄道のタンポポライナーを使う方法です。
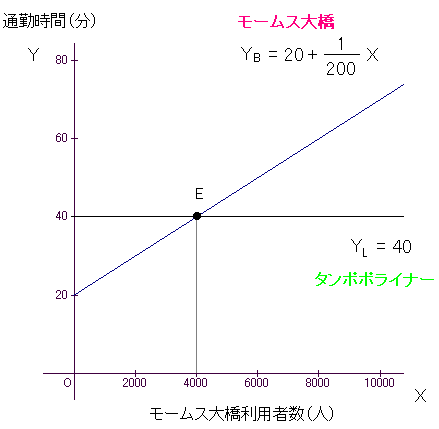
 ラッシュアワーには、島から市の中心部へ1万人が通勤します。 モームス大橋を使うと、他に車が1台もいない場合、20分で市の中心部へ着きます。 そして車が2000台増えるごとに、10分余計にかかります。 一方、タンポポライナーを使えば、所要時間40分で中心部へ行けます。 利用者が増えても、電車は増発できるので、いつでも40分で行けます。 さて、タンポポアイランドの1万人の通勤者のうち、何人がモームス大橋を車で渡り、何人がタンポポライナーを利用するでしょうか。つまり均衡点はどこでしょうか。 これは簡単です。橋の渋滞が40分になるところが均衡点です。ここからは誰も他の方法には動こうとしません。どっちに動いても40分だからです。よって均衡点は（モームス大橋4000人、タンポポライナー6000人）です。これはグラフで表すことができます。  さて、この均衡は通勤者全体にとって望ましいのでしょうか？ たとえば3000人だけがモームス大橋を使う場合を考えてみましょう。 この場合、モームス大橋利用者は YB = 20+(1/200)*3000 = 35 (分) かかることになります。一方、タンポポライナー利用者は7000人になりますが、 所要時間は40分で変わりません。 3000人が 40-35 = 5分 得することになるので、全体では15000分の短縮（節約）になります。 よって、1000人がタンポポライナーに切りかえれば、全体では15000分節約できるので、 X=4000 は最も望ましい点とは言えません。 では最も望ましい点はどこなのでしょうか。 まず、モームス大橋利用者が4000人より1人でも多くなると、40分以上かかることになるので、全体では節約できません。よってまず X≦4000 でなければいけません。 この条件のもとで、 節約できる時間は、 T = X (40-Y) (分) になります。 よってこれは、X≦4000 で T = X (40-Y) の最大値を求める問題になります。 
T  以上のように X=2000 のとき T=20000 が最大値です。つまり、モームス大橋の利用者が2000人のときが最も望ましく、通勤者全体で20000分短縮できます。 通勤者全体にとって最も望ましい点が X=2000 であるのに対し、実際の均衡点は X=4000 です。通勤者のそれぞれが利己的に行動した結果、通勤者全体でマイナスになっているのです。よってこれは多人数版の「囚人のジレンマ」といえます。
◆どうやってこの囚人のジレンマを解決すればよいのでしょう。どうやって利用する人の数を減らせばよいのでしょう。 考えられる１つの方法はモームス市が橋の利用料金をとることです。 そしてその料金収入を何らかの形でタンポポアイランドに還元すれば、結果として橋を使う島民が橋を使わない島民にお金を支払うのと同じことになります。ところで市が利用料金をとるのは課税と同じです。 一般に課税は囚人のジレンマの解決に有効です。
◆参考文献
|
