ケーキの分割
|
ここに小学生の兄弟がいるとします。ある日母親がケーキを買ってきました。 兄弟のために２つ買ってきたのですが、母親がおもわずひとつ食べてしまいました。残りは１個です。この最後のケーキの分配が問題になります。 あらかじめ母親が半分に切っておくこともできますが、どうせ「こっちのほうが大きい」とケンカになりそうです。兄弟が学校から帰ってきました。今日は運が悪いことに、兄弟はケンカをして口もきいていないという状況でした。 こういうとき、どのようにすればいいのでしょう？ 一番よい方法は、「兄に切らせ、弟が先に選ぶ」というものです。 兄は一方を大きく切ってしまうと、弟にそっちを取られます。一方を小さく切っても、やはり大きい方を取られます。けっきょく兄は、半分に切るしかありません。 じつは、これはミニマックス定理のもっとも簡単な例なのです。 ゲーム理論では、これを2人ゼロサムゲームといいます。 ゼロサムゲームは合計(SUM)がゼロになるゲームです。つまり一方の得が、必ずそのままもう一方の損になるゲームです。いいかえれば、全面戦争です。相手が負けるとき、自分が勝ちます。協調はありえません。 このゲームをテーブルで表してみます。  切り方はいろいろあるのですが、単純化のために、「半分かそうでないか」の2通りにします。また、カンペキに半分に切ることはできないので、片方がほんの少しだけ大きくなるとします。 あたりまえですが、選ぶ方は必ず大きいほうを選びます。よって左の列を選びます。 これを前提にして、切る方は戦略を選びます。もちろん切る方は「小さい方」より「半分よりほんのちょっと小さい」を望むはずなので、できるだけ同じ大きさに切ります。つまり上の行を選びます。 技術的に言いかえると、こうです。 切る側は、2つの行の2つの最小値、「半分よりほんのちょっと小さい」と「小さい方」のうち、 最大のものである「半分よりほんのちょっと小さい」を選びます。これを最大の最小値＝マクシミン(maximin)といいます。これは自分の利得の最低水準を上げようということです。 選ぶ側は、2つの列の2つの最大値、「半分よりほんのちょっと小さい」と「大きい方」のうち、 最小のものである「半分よりほんのちょっと小さい」を選びます。 これを最小の最大値＝ミニマックス(minimax)といいます。 これは自分の防ぎきれない損失をできるだけ小さくしようということです。 ミニマックス定理でマクシミンとミニマックスの値が一致する点のことを「鞍点（あんてん）」といいます。 鞍（くら）の形をした峠の中心にある点を思い浮かべてください。峠を通る旅人にとっては、そこは高さが最大のところです。一方、尾根伝いに移動するヤギにとっては、高さが最小のところです。これに似ているので「鞍点」といいます。
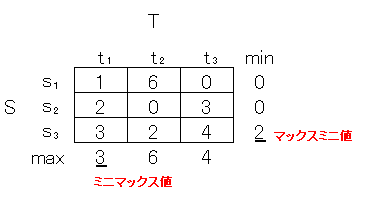
◆安全第一 つぎのようなゼロサムゲームを考えてみてください。 テーブルには S の利得が書いてあります。 ２人が同じように悲観的な発想をするとしましょう。 つまり S は、自分の最小利得が最大になるようにし、 T は自分の最大損失が最小になるようにします。 このときマックスミニ値とミニマックス値が一致しないので、 このゲームは鞍点をもたないことがわかります。
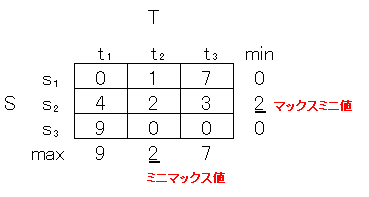
つぎのゲームはどうでしょう？これは鞍点をもちます。 (S, T) = (s2, t2) これがゲームの均衡点です。
マックスミニ戦略とミニマックス戦略は同じ悲観的な考え方です。 相手の最大利得を最小にするというのは、 符号をマイナスに変えれば、自分の最小利得を最大にすることと同じです。 （下のゲームで言うと、 -9, -2, -7 を比較して -2 をとると考える）。 そこで マックスミニ戦略とミニマックス戦略は まとめてミニマックス戦略と呼ばれます。
◆参考文献
|
