小学生のころ、階段じゃんけんをやりました。 自分が大物狙いでパーにこだわると、相手はチョキを出すようになります。そして、自分は、相手がチョキばかり出すことに気付いて、こんどはグーを出そうとします。するとこんどは相手がパーを出し・・・と堂々巡りになります。ゲーム理論は、このゲームに関して、きわめてクリアーな解答を与えます。このゲームには負けない方法があるのです。それでは見てみましょう。 いま2人でやる階段じゃんけんを考えます。グーで1段、チョキで2段、パーで5段とします。 プレーヤー（自分、相手）の利得は下の表のようになります。 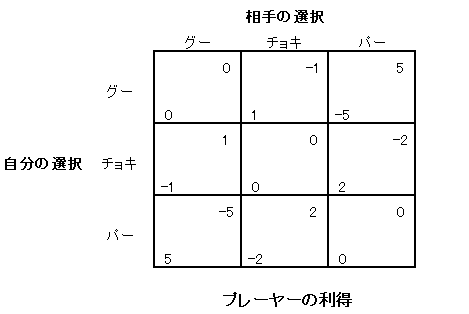それではこのゲームの戦略を考えます。 まず、自分が グーを出す確率を p チョキを出す確率を q パーを出す確率を 1-p-q とします。 すると期待値の考え方から、 相手の期待利得は グーを出すと： 0p+1q-5(1-p-q) チョキを出すと： -1p+0q+2(1-p-q) パーを出すと： 5p-2q+0(1-p-q) になります。 では、自分が負けないためにはどうすればよいでしょうか？「相手がどんな手を出してきても負けない」というのは、すなわち「相手は何を出しても期待利得が0になる」ということです。 だから、上の3式をすべて0にするような p,q の値を見つければよいことになります。よって、 0p+1q-5(1-p-q)=0 -1p+0q+2(1-p-q)=0 5p-2q+0(1-p-q)=0 この連立方程式を解くと、 p=1/4 q=5/8 1-p-q=1/8 相手が何を出そうと、自分がこの確率（グー：チョキ：パー＝2：5：1）で出せば、相手の期待利得は等しく 0 になります。 だから、 ある戦略をとることにより、相手の利得を 0 にすることができる。つまり、負けない。 ということです。 このような点は一種の定点といえます。ゲーム理論ではこのような点のことを均衡点といいます。 また、このような点を「ゲームの解」ともいい、以上のような過程を「ゲームの解を求める」といいます。 このゲームは対称形のゼロサムゲームです。つまりお互い対等の条件にあります。 よってこの自分にとって最善のミックスは、相手にとっても最善のミックスになります。つまり相手も、グー：チョキ：パー＝2：5：1の割合で出せばよいのです。この均衡においては、自分も相手も期待利得はゼロです。そして、このような期待利得ゼロの均衡は、対称形をしているゼロサムゲームでは、必ず成立します。 ◆参考文献 『エール大学式ゲーム理論の発想法―戦略的思考とは何か』　 アビナッシュ・ディキシット、バリー・ネイルバフ、TBSブリタニカ、1991年 THINKING STRATEGICALLY (1993)