 テニスのかけひき |
 |
|
今回はテニスのかけひきについて考えます。
いま、プレーヤーの強さが下のテーブルで表されるとします。
テニスは利害が完全に対立するゼロサムゲームなので、一方のプレーヤーのみに注目できます。ここではレシーバー側からみてみます。
表からわかるように、レシーバーはフォアハンドのほうが得意です。 ではサーバーはバックを重点的に狙ったほうがよいのでしょうか。 また、それならレシーバーはバックを重点的に守ったほうがよいのでしょうか。 またまたそれなら、サーバーはフォアを狙ったほうが・・・と堂々めぐりになります。 こういう問題に一定の答えを与えるのがミックス戦略とよばれるものです。 結論から言うと、サーバーは６割バックを狙えばよく、レシーバーは７割バックを守ればよいのです。また、このときのレシーブ成功率は48％で、これがゲームの均衡になります。
◆ミックス戦略 まず最悪な打ち方を考えてみます。いま、 サーバーが常にフォアを狙うとします。するとレシーバーは常にフォアを予想するので、フォアに動きます。このときレシーブの成功率は90％になります。 あるいはサーバーが常にバックを狙うとします。 するとレシーバーは常にバックを予想するので、バックに動きます。 このときレシーブの成功率は60％です。 当然、フォアとバックを打ち分ける必要があります。
いま仮にサーバーがフォアとバックを半々に打ち分けるとします。この場合、レシーバーはフォアへ動くとレシーブ成功率は 90*0.5+20*0.5=55 です。バックへ動くとレシーブ成功率は 30*0.5+60*0.5=45 です。 そこでこれはサーバーにとって一歩前進といえないでしょうか。 なぜならいつも同じ方向を狙うより、レシーブの成功率が下がったからです。 このように、サーバーは狙いを分散させミックスすることにより、レシーブ成功率を下げることができます。そこで問題はどういうミックスが最善かということです。 ◆サーバーのミックス戦略 サーバーのミックスに対するレシーバーの動きを考えてみます。
サーバーのフォア狙いの比率を x とします。 つまりフォア：バック ＝ x：1-x です。
レシーブ成功率は これをグラフにするとつぎのようになります。
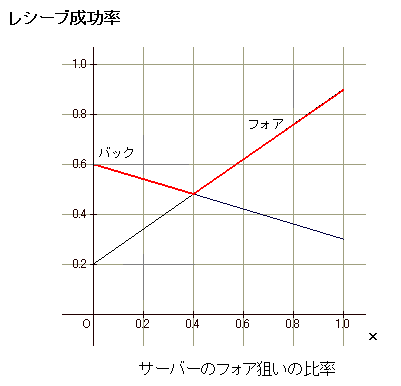
交点は x=0.4, y=0.48 レシーバーは、 サーバーのフォア比率 x ＜ 0.4 ではバックに動くほうがよく、 x ＞ 0.4ではフォアに動いたほうがよいことがわかります。 つまり、サーバーのミックス率が x≠0.4 のときに、 レシーバーが相手のミックスに応じて的確に動くと、 レシーブ成功率は常に48％より上になります。 しかし、サーバーがミックスを x=0.4 にすると、 レシーブ成功率は常に48％になります。 じつはこれがサーバーの最適戦略なのです。 （ここでサーバーは最大損失を最小にする打ち方になっている＝ミニマックス戦略） ◆レシーバーのミックス戦略 レシーバーのミックスに対するサーバーの狙いを考えてみます。
レシーバーのフォア待ちの比率を p とします。 つまりフォア：バック ＝ p：1-p です。
レシーブ成功率は グラフはつぎのようになります。
交点は p=0.3, q=0.48 サーバーは、 レシーバーのフォア待ち比率 p ＜ 0.3 ではフォアを狙うほうがよく、 p ＞ 0.3ではバックを狙うほうがよい ことがわかります。 つまりレシーバーのミックス率が p≠0.3 のときに、 サーバーがレシーバーのミックスに応じて的確に動くと、 レシーブ成功率は常に48％より下になります。 しかし、レシーバーがミックスを p=0.3 にすると、 レシーブ成功率は常に48％になります。 じつはこれがレシーバーの最適戦略なのです。 （ここでレシーバーは最小利得を最大にする打ち方になっている＝マックスミニ戦略） ◆ミニマックス定理 さてここでおもしろいことに気付きませんでしたか？ それは2人とも成功率が48％になるということです。 サーバーは48％という最小値におさえこみました。 レシーバーは48％という最大値をつかみました。 お互いの利害が完全に対立する2人ゲームは、すべてこの特性をもちます。 これをミニマックス定理といいます。
ミニマックス定理
◆参考文献
|
