あいとのぞみ
|
前回の「ナッシュ均衡」で述べたように、ゲーム理論ではナッシュ均衡をゲームの解とするのですが、
問題なのはナッシュ均衡が複数存在するときです。今回はそれを見ていきます。
仲良しコンビのアイとノノが金曜日の午後の過ごし方を決めなければなりません。 アイはパチンコに行くほうがよく、ノノは映画を見に行くほうがよいです。 別々に行動することもできますが、これは２人にとってあまりよくありません。 このゲームは下のテーブルで表されます。
このゲームでは、誰も絶対優位の戦略をもたないので、ナッシュ均衡を求めます。 ゲームの結果は４つあるので、それぞれの状況を確認してみましょう。 まず、左上のマスです。これは 「相手の戦略に対してお互いが最善を尽くしている状況」なんじゃないでしょうか。 なぜなら、アイはノノのパチンコという戦略に対してベストの戦略であるパチンコをとっていますし、同時にノノはアイのパチンコという戦略に対してベストの戦略であるパチンコをとっています。 左下のマスはどうでしょう。これはちがうとおもいます。 なぜならアイはノノのパチンコという戦略に対してベストの戦略をとっていませんし、 ノノもアイの映画という戦略に対してベストの戦略をとっていません。 右上のマスも同様に考えてダメです。 しかし右下のマスはいいんじゃないでしょうか。 アイはノノの映画を前提にしたとき、映画がベストですし、 ノノはアイの映画を前提にしたとき、映画がベストです。 以上より、左上のマスと右下のマスがナッシュ均衡であることがわかりました。 このように、 このゲームには２つのナッシュ均衡があるのです。しかし どっちの均衡が選ばれるかは何とも言えず、 アイとノノがどうなるかはまったくわかりません。
◆ナッシュ均衡の見つけ方にはコツがあります。 上のテーブルをコピーしてペイントツールなどに移してみてください。
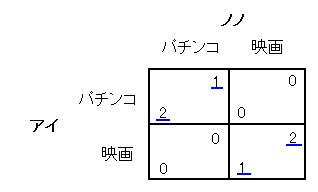
ノノのパチンコに対して、アイはパチンコがいいので利得2に下線を引きます。 ノノの映画に対しては、アイは映画がいいので利得1に下線を引きます。 同様にして、 アイのパチンコに対して、ノノはパチンコがいいので利得1に下線を引きます。 アイの映画に対しては、ノノは映画がいいので利得2に下線を引きます。 線が2本そろっているマスがナッシュ均衡です。 ◆参考文献
|
