支配される戦略
|
「消去法」という方法があります。
ありえない選択肢を消していくやつですね。
問題を効率良く解くために使います。
選択肢が多い場合には欠かせません。
明らかに間違ったもの、劣ったものをどんどん消していくのですね。
つぎのようなゲームを考えてみてください。
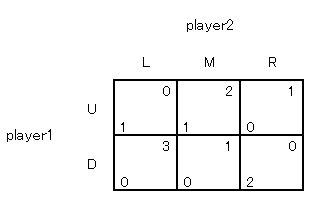
なんか複雑ですよね。これは消去法で解きます。 R は明らかに M より劣っていますよね。 R が選ばれることはありえないです。 そこで R を消去します。 （ R を「支配される戦略」といいます。） すると ゲームはつぎのように小さくできます。
こうなったらもう簡単ですよね。プレーヤー1は U が絶対優位の戦略になって U を選びます。プレーヤー2は M を選びます。 ▼つぎの問題も同じように解けます。
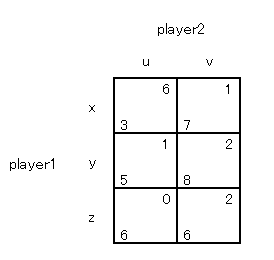
x が y に支配されるので消去します。
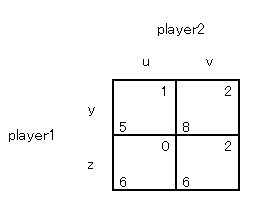
プレーヤー2は v が絶対優位の戦略になって v を選びます。プレーヤー1は y を選びます。 ▼最後にこの問題はどうでしょう。
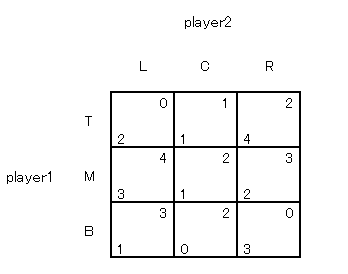
まず B が T に支配されるので消去します。
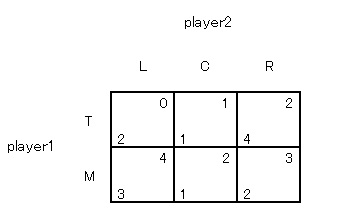
つぎに C が R に支配されるので消去します。
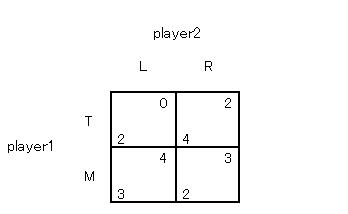
絶対優位の戦略がないのでナッシュ均衡を求めます。
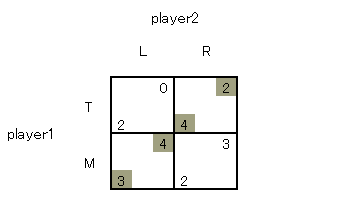
(player1, player2) = (M, L), (T, R) がナッシュ均衡です。
つぎのような命題があります。このような消去法で ナッシュ均衡が消されることはないのでどうぞ安心して消去してくださいということです。
（記述の仕方に関しては付録２（ナッシュ均衡）を見てください。） ◆参考文献
|
