合理的なハムスター
|
大きいハムスターの太郎と小さいハムスターのチビコ。
２匹は同じ部屋に住んでいます。
おやつの時間には大好きなポッキーをもらいます。
部屋の片隅についているレバーを押すと、
部屋の反対側の片隅にポッキ―が６本だけ出てくるのです。
２匹はポッキーが大好きなのでいつも取り合いになります。 このとき、レバーを押したほうは、ポッキ―にたどりつくまでに、もう一匹にほとんどを食べられてしまいます。 実際に奪い合いになったときは、 大きい太郎が小さいチビコをはね飛ばして追い払うことができます。 ゲームの構造はつぎのようになっています。 太郎がレバーを押した場合、太郎がポッキ―にたどりつくまでに チビコが６本のうち５本を食べてしまいます。 チビコがレバーを押した場合、太郎が６本すべてを食べてしまいます。 同時にレバーを押してしまった場合は、 すばしっこいチビコが先にポッキ―にたどりついて ２本を食べることができます。 また、レバーを押して部屋の端から端まで走るのにポッキ―0.5本分のコストがかかるとします。 さて２匹はゲーム理論家であるとしましょう。 いままで考えてきたようなテーブルや先読みを用いて 戦略を決めるのです。このとき２匹はどういう行動に出るのでしょう。 まず、２匹がレバーを押すか押さないかの戦略をもつので ２×２のテーブルができます。 まず、２匹とも押さない場合、ポッキ―はもらえないので 利得はともに 0 です。 太郎が押した場合、太郎の利得は 1-0.5=0.5 、チビコの利得は 5 です。 チビコが押した場合、太郎の利得は 6 、チビコの利得は -0.5 です。 ２匹が同時に押してしまった場合の利得は、 先にたどりつくチビコ 2-0.5=1.5 、 遅れる太郎 4-0.5=3.5 です。 以上を整理してつぎのようなテーブルになります。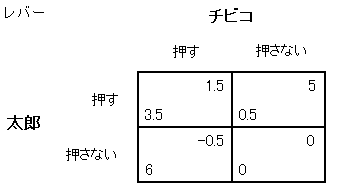  まず、この同時進行ゲームにおいては、チビコが絶対優位の戦略をもつことがわかります。 よってチビコは「押さない」戦略をとります。 一方の太郎はそれを読んで戦略を考えます。 チビコが押さない場合、太郎が押すと利得は0.5 、押さないと0なので、 太郎は押したほうがよいです。つまり太郎は「押す」戦略をとります。 これが太郎のチビコに対する最適反応です。 よってゲームの均衡はテーブルの右上、（太郎、チビコ）＝（押す、押さない）になります。 これは驚きました。 か弱いチビコが利得5をとり、太郎はたったの0.5しか利得がありません。 いやその前に労力を使った太郎がたったの0.5で、 何もしなかったチビコがほとんどのポッキ―をとってしまうのです。 そしてこれは２匹が合理的な行動をとることによって生まれる結果なのです。
今回紹介したのは「箱の中の豚」「合理的な豚」の名前で知られるゲームのハムスター版です。直観的に納得いかない結果がおもしろいですよね。 ゲーム理論家であるという仮定をしているので、ありそうもない結果だと おもわれるかもしれません。しかし、驚いたことに、 動物学者が実際に豚を使って同じ実験をしてみると、 豚は試行錯誤を繰り返した後、このゲームの「解」を発見し、「合理的な結果」へ収束していったのです。 まるで豚がゲーム理論家のような行動をしたのです。 世の中には一方的に負担しているいっけん利他的な関係って 多いですよね。でもそれらはたいてい そのほうが自分が利益を得られるからという合理性の結果 なのです。
◆ このゲームを囚人のジレンマと比べてみましょう。 このハムスターのゲームでは、囚人のジレンマと違って、 個人合理性と集団合理性の対立がありません。 囚人のジレンマでは、 一方のプレーヤーの状態を改悪することなく結果を変えることができました （これを「パレート劣位」といいます）。 しかしハムスターのゲームでは 一方のプレーヤーの状態を改悪することなく結果（太郎、チビコ）＝（0.5、5）を変えることができません（パレート効率的）。 ◆ 太郎はチビコの「押さない」戦略を前提にしたとき、「押す」が最善の戦略です。 いっぽうチビコは、太郎の「押す」戦略を前提にしたとき、「押さない」が最善の戦略です。このように、 すべてのプレーヤーがおのおの自分以外のプレーヤーの行動に対して最善を尽くしている状況をナッシュ均衡といいます。 このゲームのナッシュ均衡は（押す, 押さない）です。 ここでは互いに戦略を変える誘因がありません。 相手の戦略を前提にしたとき、自分だけ戦略を変えてみても利得が上がらないからです。 しかし他の戦略の組合せでは戦略を変える誘因があります。たとえば（押す, 押す）では、チビコは「押さない」戦略に変える誘因があり、不安定です。（押さない, 押す）, （押さない, 押さない） も同様です。 ゲーム理論で単に均衡というと、それはナッシュ均衡のことを指します。
◆参考文献
|
