 ミルク戦争 |
 |
モームス市の学校給食の牛乳は
「なっち乳業」と「かおりん牧場」のただ２つの企業によって生産されています。
いまなっちが x 単位、 かおりんが y 単位生産するとします。 すると総供給量は x+y です。 供給量が多いほど、価格は下がります。 そこで a を定数として、 p = a - (x+y) で価格が決まるとします。 また、1単位生産するのにかかる費用は c （定数）であるとします。 なっち乳業の利潤は
π1 (x, y) 企業は利潤を最大にするのが目的なので、この関数の最大値を与える x を考えます。 いま、y を固定し、これを x の関数であると考えます。 グラフの形を考えましょう。これは上に凸の関数です。そして x≧0 に注意し、軸の位置で場合分けします。 つまり、軸が x＜0 の位置にある場合は x=0 で最大値をとり、 軸が x≧0 の位置にある場合は x = (a-c-y)/2 で最大値をとります。
まとめると なっち乳業は かおりん牧場 π2 は 、 x と y を入れ換えて、
じつはこれは生産量を戦略とするゲームです。 上の場合分けをつぎのように読みかえてみてください。すなわち、
なっちは
かおりんは、 x と y を入れ換えて、 このゲームのナッシュ均衡を求めましょう。 ナッシュ均衡とは、お互いが最適反応をしている戦略の組合せでした。 ここで戦略の組合せというのは生産量の組です。 すなわち x と y の組であり、 xy平面上の点です。 なっちについて考えましょう。 (a-c-y)/2 ＜ 0 ⇔ a-c-y ＜ 0 ⇔ y ＞ a-c の場合 x = 0 が最適反応で、 y ≦ a-c の場合 x = (a-c-y)/2 ⇔ y = -2x+a-c で定まる x が最適反応になります。この1次直線によって、かおりんの1つの y に対応してなっちの1つの x が決まるのですね。 そこでなっちの最適反応はつぎのグラフで表現できます。
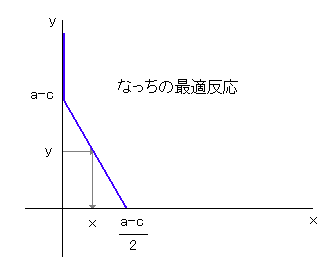
かおりんについても同様に考えることができます。 x ＞ a-c の場合 y = 0 が最適反応で、 x ≦ a-c の場合 y = (a-c-x)/2 で定まる y が最適反応になります。
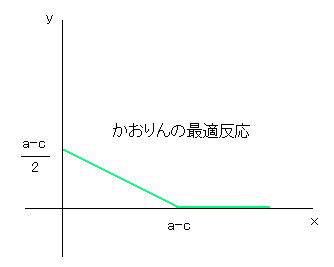
では、お互いに最適反応となる x, y の組合せはどのように求めるのでしょう。 それは２つの曲線の交点ではないでしょうか。 なぜならば、上の曲線はなっちの最適反応となる (x, y) を示しており、 下の曲線はかおりんの最適反応となる (x, y) を示しています。 ということは２つの曲線の交点となる (x, y) というのは、 なっちとかおりんがお互いに最適反応している点ですよね。 しかもそれはただ1点だけです。 これがこのゲームのナッシュ均衡です。
交点は -2x+a-c = (a-c-x)/2 を解いて、 あるいは幾何的に考えてみます。 よく見ると交点は三角形の重心ですよね。 重心は中線を 1：2 に内分します。 そこで線分の比を考え交点の座標は ( (a-c)/3, (a-c)/3 ) です。
◆参考文献
|
