 ナッシュ均衡２ |
 |
|
つぎのようなゲームを考えてみてください。
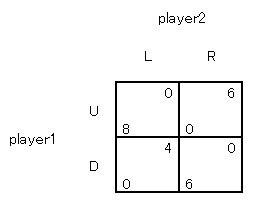
このゲームにはナッシュ均衡がありません（下図）。 もし2がLを選べば1はUを選ぶ。1がUを選べば2はRを選ぶ。2がRを選べば1はDを選ぶ。 1がDを選べば2はLを選ぶ・・・。 これで論理の循環が１周します。 堂々巡りになるのですね。
そういえば「階段じゃんけん」「テニスのかけひき」でも同じようなことになっていました。 だったらこのゲームでもミックス戦略を考えればいいんじゃないでしょうか。 じつはこのゲームは、純粋戦略ではナッシュ均衡はないのですが、混合戦略まで考えるとナッシュ均衡があるのです。
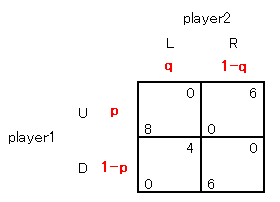
いま、ミックス比率を図のようにすると、
左上のマスになる確率は pq です。（ただし 0≦p≦1 , 0≦q≦1 ）
player1の期待利得は
player2の期待利得は
です。
1の期待利得をpについて整理します。
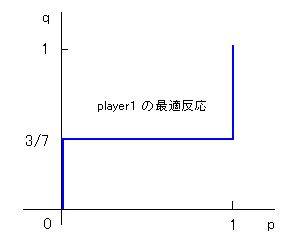
いま、2が -6+14q ＜ 0 となるようなqを使ってきたとしたらどうなるでしょう。 このとき、上式は右下がりの1次直線になるので、 p=0 のとき最大値をとります。 -6+14q ＞ 0 のようなqではどうでしょう。 この場合、上式は右上がりの直線になり、p=1 のとき最大値をとります。 ところが、 -6+14q=0 のとき、すなわち q=3/7 のときはどうでしょう。 このとき1の期待利得はpの値に関わらず、 -6(3/7)+6 = 24/7 になります。 これはいいかえると、
q ＜ 3/7 のときは p=0 が最適反応 ということです。 これはグラフにかくとつぎのようになります。
player2についても同様に考えます。
2の期待利得をqについて整理します。
いま、1が 4-10p ＜ 0 となるようなpを使ってくるとします。 このとき、上式は右下がりの1次直線になるので、 q=0 のとき最大値をとります。 4-10p ＞ 0 のようなpでは、上式は右上がりの直線になり、q=1 のとき最大値をとります。ところが、 4-10p=0 のときすなわち p=2/5 のときは、 2の期待利得はqの値に関わらず 6(2/5) = 12/5 になります。 これはいいかえると、
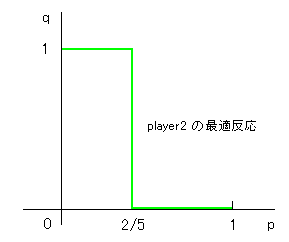
p ＜ 2/5 のときは q=1 が最適反応 になります。
ナッシュ均衡とはお互いに最適反応をしている戦略の組合せでした。 ２つの曲線を同じpq平面の上にかいてみます。 いろいろな点を考えたとき、お互いに最適反応をしている 点というのはないでしょうか。 まず、いずれかが最適反応をしているのは色のついた線の上の点です。 そしてこのうち、交点の (2/5, 3/7) だけはお互いに最適反応している点です。
ゲーム理論はつぎの存在定理に支えられています。 要はどんなゲームにもナッシュ均衡があるということです。 すごい話ですね。
（記述の仕方に関しては付録２（ナッシュ均衡）を見てください。） ◆参考文献
|
