 ミルク戦争２ |
 |
|
「ミルク戦争」は同時に生産量を決定する同時進行ゲームでしたが、今回は「なっち乳業がまず生産量を決めて→そのあとにかおりん牧場が生産量を決める」という交互進行ゲームを考えます。
このゲームは交互進行ゲームなのでツリーで表現することができますが、それぞれのプレーヤーの戦略は無限にあるので、下のようにして表すことにします。 
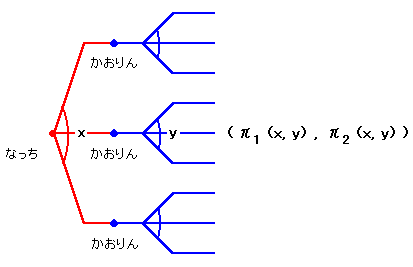
さて、交互進行ゲームなので例によって後ろから解くことを考えます。 まず、かおりんの最適反応はすでに調べたように、
x ＞ a-c の場合 y = 0
です。
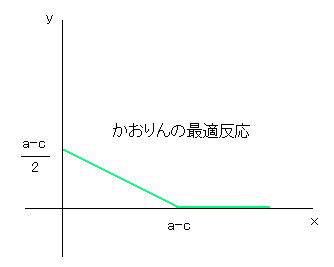
そして、なっちはこれを先読みして戦略を決めます。
（１）いま、なっちが x ＞ a-c となる x を使うとしましょう。するとかおりんの最適反応は y = 0 です。これを前提にしてなっちは x を決めます。すなわちなっちは
π1 (x, y) = (a-x-y)x - cx の y に 0 を代入したあとで、 x を決めます。
π1 (x, y) この関数をグラフにかくと下のようになります。
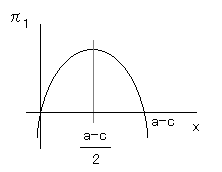
式☆は - x ( x - (a-c) ) のように変形できるので、 x軸との交点は x = 0 , a-c となります。グラフは上に凸、頂点のy座標は正です。（ところで a＞c です。 a は最高価格ですが、これが費用 c 以下だとすると、はじめから生産しません。） そして変域 x ＞ a-c に注意して最大値を求めると、これは0をこえないことがわかります。 （２）つぎに、なっちが x ≦ a-c となる x を使うとしましょう。するとかおりんの最適反応は y = (a-c-x)/2 です。これを前提にしてなっちは x を決めます。すなわちなっちは
π1 (x, y) = (a-x-y)x - cx で y = (a-c-x)/2 としたあとで、 x を決めます。
π1 (x, y)
この関数をグラフにかくと下のようになります。
式☆☆はやはり x ( (a+c-x)/2 - c ) = x ( (a-c-x)/2 ) のように変形できるので、 x軸との交点は x = 0 , a-c となります。 そして変域 x ≦ a-c に注意して最大値を求めると、これは (a-c)2/8 （ ＞ 0） になります。
こうしてなっちはx ≦ a-c となる x を使うのがよいことがわかって、 そしてその x が (a-c)/2 ならば最適であるということがわかりました。 同時進行ゲームではなっちの生産量は (a-c)/3 でしたが、交互進行ゲームではその50％増しで作るとよいことがわかりました。かおりんはなっちの生産量を見たあと、 y = (a-c - (a-c/2))/2 = (a-c)/4 を作ります（25％減）。 「なっちが (a-c)/2 を作る → かおりんが (a-c)/4 を作る」。 これがこのゲームの部分ゲーム完全均衡です。
◆参考文献
|
＜ なっちもういっぱい作ったべさ。かおりんとこは少しでいいべさ。
＜ ・・・
