|
「あいとのぞみ2」「脅しの信憑性」で部分ゲーム完全均衡という新しい概念が出てきました。しかし、これもまたナッシュ均衡なのです。
まず、ツリーのゲームというのは必ずテーブルに直すことができます。
「あいとのぞみ2」のゲームを考えましょう。
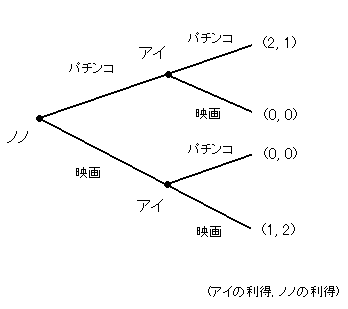
これはまずノノが動いて、その後にアイが動くというゲームでした。
ゲームを始める前のアイの頭の中をのぞいてみましょう。
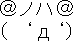 |
ノノがパチンコできたらパチンコにするか映画にするか、、、これはパチンコやな。
ではノノが映画できたらパチンコにするか映画にするか、、、これは映画やな。
|
上の点ではパチンコを選び、下の点では映画を選ぶのですね。これは
(上の点での選択−下の点での選択)で表すとすると、
(パ−パ)(パ−映)(映−パ)(映−映)という戦略の中から
(パ−映)という戦略を選ぶということです。
そこでこれは、アイが4つの戦略をもち、ノノが2つの戦略をもつゲームとして考えることができます。
◆部分ゲーム完全均衡
ナッシュ均衡を求めます。このゲームには3つのナッシュ均衡があることがわかります。
じつは部分ゲーム完全均衡とは、これらのナッシュ均衡のうちの、ある特別な1つだったのです。
いったいどういうことでしょう?これはツリーに戻って考えます。
1行1列(左上)のナッシュ均衡についてよく考えてみましょう。これはゲームツリーでかくとつぎのような経路です。でもこれはよく見るとおかしいんじゃないでしょうか。というのはアイが下の点でパチンコを選択するのは合理的でないからです(利得0と1を比較して0を選んでいる)。

同様に4行2列(右下)のナッシュ均衡もおかしいです。
アイは上の点で映画を選択するのは合理的でないからです(利得2と0を比較して0を選んでいる)。
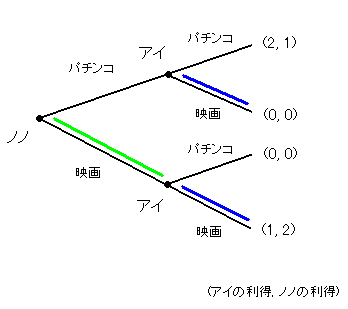
そこで
唯一合理的になっているのが2行2列のナッシュ均衡です。アイは上の点ではパチンコを選び、下の点では映画を選ぶのが合理的です。またこのときノノが映画を選ぶのは合理的です。
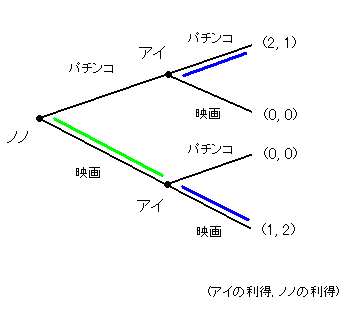
そういうわけで、
ナッシュ均衡のうち、すべての点でプレーヤーが合理的に行動しているものが
部分ゲーム完全均衡だったのです。
◆戦略
じつはゲーム理論で戦略というのは「行動計画」のことです。ゲームを始める前にあれこれと考えるものを戦略というのです。
これまで見てきた同時進行ゲームでは、とくにこのことを意識する必要はなかったですが、交互進行ゲームや繰り返しゲームでは注意が必要になります。
もう一度アイの頭の中を見てみましょう。
 |
ノノがパチンコできたらパチンコにするか映画にするか、、、これはパチンコやな。
ではノノが映画できたらパチンコにするか映画にするか、、、これは映画やな。
|

このゲームでは、アイの戦略は4つ考えられます。
すなわち
1. 「ノノがパチンコできたらパチンコ、ノノが映画できたらパチンコ」
2. 「ノノがパチンコできたらパチンコ、ノノが映画できたら映画」
3. 「ノノがパチンコできたら映画、ノノが映画できたらパチンコ」
4. 「ノノがパチンコできたら映画、ノノが映画できたら映画」
言葉で書くと非常に複雑ですが、これはツリーの上の点と下の点でとる行動の組合せ
です。4×2のテーブルにはこれらが省略して書かれています。
 <
うちの戦略はこうもいえるで。
1. 「ぜったいパチンコ」、 2. 「ノノに合わせる」、 3. 「ノノの逆」、 4. 「ぜったい映画」 <
うちの戦略はこうもいえるで。
1. 「ぜったいパチンコ」、 2. 「ノノに合わせる」、 3. 「ノノの逆」、 4. 「ぜったい映画」
|
こういうふうに戦略を考えることによって、交互進行ゲームや繰り返しゲームも「ナッシュ均衡」で統一的に考えることができます。
(すでに「おうむ返し」という繰り返しゲームの「戦略」を見ましたが、これはプレーヤーの「行動計画」です。)
◆リファインメント
このゲームでは仮にアイが「映画なんかぜったい行かへん!」と言ったとしても
それは信憑性のない脅しです。
アイの「ぜったいパチンコ」戦略とノノの「パチンコ」戦略の組はナッシュ均衡にはなっても実際の結果としてはありそうもないのです。
そこで部分ゲーム完全均衡というのはこういう信憑性のない脅しを見抜くための概念です。
部分ゲーム完全性などを調べることでありそうもないナッシュ均衡を排除することを「精緻化(refinement)」といいます。
◆参考文献

|
 ナッシュ均衡3
ナッシュ均衡3
 ナッシュ均衡3
ナッシュ均衡3