|
今回は囚人のジレンマを2回繰り返すゲームを考えます。
前回のように後ろ向きに考えれば、まず2回目のゲームは1回きりの囚人のジレンマと同じなので (裏切り, 裏切り) 、そしてそれがわかっているので1回目のゲームでも (裏切り, 裏切り) というふうになります。
今回はこの2回繰り返しゲームをツリーを使って考えてみたいとおもいます。
◆情報集合
まず1回きりの囚人のジレンマをツリーで表す方法です。
これはまず場合分けの要領で考えます。
マキが協調の場合、マキが裏切りの場合に分けるのです。
そしてそれぞれの場合でヒトミが協調の場合、ヒトミが裏切りの場合を考えます。
すると下のようなツリーで表現することができます。
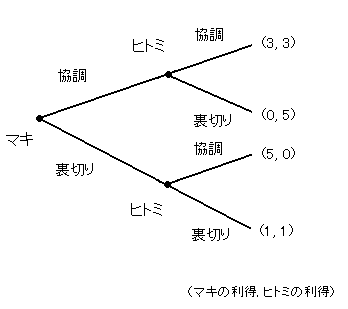
ところがこれはマキが先に動いてヒトミが後に動く交互行動ゲームと区別ができません。
囚人のジレンマではヒトミはマキの決定を知らないのです。
ツリーで言えば自分がどっちの点にいるかわからないのです。
どうすればよいのでしょう。
これは2つの点を丸で囲んでおけばよいのです。
こうすれば囚人のジレンマをツリーで表現することができます。

これはマキを先頭にしてかきましたが、ヒトミを先頭にしてかいてもよいです。
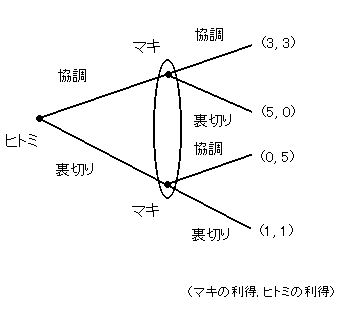
ここで点を丸で囲んだものを情報集合といいます。
◆2回繰り返しゲーム
まず、簡略化のために、1回きりの囚人のジレンマを下のようにかいておきます。
 (マキを赤、ヒトミを青、協調を c 、裏切りを d としました。
また情報集合はグレーの線で表しています。)
(マキを赤、ヒトミを青、協調を c 、裏切りを d としました。
また情報集合はグレーの線で表しています。)
では、2回の繰り返しゲームをツリーで表す方法を考えます。
これは、上のツリーの4つの末端に、上と同じツリーをくっつければよいのです。
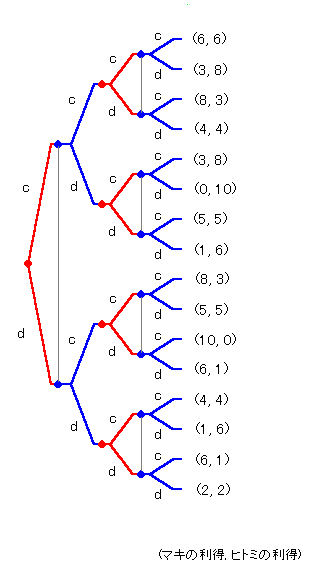
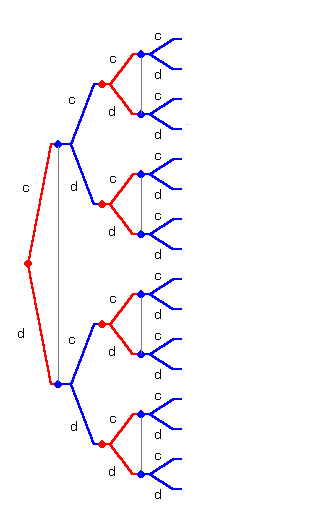 そして新しい利得を考えます(下図)。
たとえば一番上は1回目のゲームで (協調, 協調) 、2回目のゲームで (協調, 協調) ということなので、
マキの利得は 3+3=6 , ヒトミの利得は 3+3=6 となっています。
そして新しい利得を考えます(下図)。
たとえば一番上は1回目のゲームで (協調, 協調) 、2回目のゲームで (協調, 協調) ということなので、
マキの利得は 3+3=6 , ヒトミの利得は 3+3=6 となっています。
◆部分ゲーム
ここで、ツリーの右上の部分
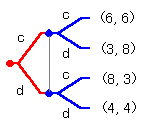
を見てください。
いま、この部分だけをゲームとして分析することができます。
すなわちつぎのゲームです。
そして、このゲームでナッシュ均衡は(裏切り, 裏切り)です。
このようにツリーの中で切り離して分析できる部分を部分ゲーム(subgame)といいます。ツリーの中には全部で5つの部分ゲームがあります。
全体のゲームも部分ゲームといいます。
上から2番目の部分ゲームも同様に考えます(下の4つのツリーのうち左下のツリー)。
マキは c をとると 3 or 0 、 d をとると 5 or 1 なので d が支配戦略(絶対優位の戦略)です。
ヒトミも c をとると 8 or 5 、 d をとると 10 or 6 なので d が支配戦略です。
したがって (d, d) がナッシュ均衡になります。
上から3番目、4番目の部分ゲームも同様に考え (d, d) がナッシュ均衡になります。

◆部分ゲーム完全均衡
最後に、いちばん左の点から始まる部分ゲーム、すなわち全体のゲームを考えます。

ところが、上で求めたように、すでに2回目以降のゲームの流れは決まっているので、
いちばん左の点から始まる部分ゲームというのはつぎのようにかけます。
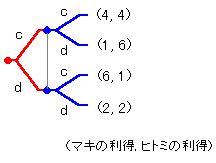
この部分ゲームでナッシュ均衡は(裏切り, 裏切り)です。
けっきょくマキもヒトミも常に裏切るというのが部分ゲーム完全均衡になります。
◆囚人のジレンマの有限回繰り返し
3回繰り返しゲームを考えます。
まず第3期から始まる16個の部分ゲームは(裏切り, 裏切り)です。
最初の縮約で2回繰り返しゲームと同じ利得構造になります。
よって第2期から始まる4個の部分ゲームは(裏切り, 裏切り)になります。
つぎの縮約で1回きりの囚人のジレンマと同じ利得構造になります。
よって第1期から始まる1個の部分ゲームは(裏切り, 裏切り)になります。
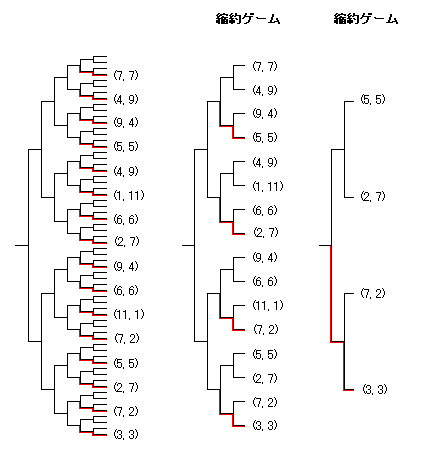
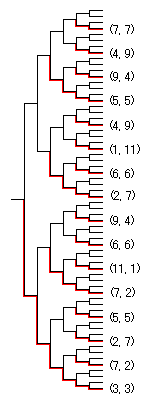
こうして
3回繰り返しゲームでも「常に裏切る」の組が部分ゲーム完全均衡になることがわかります。
4回繰り返しゲームでも5回繰り返しゲームでも同じように考えていけます。
囚人のジレンマの有限回繰り返しでは
それぞれのプレーヤーが常に裏切るというのが
唯一の部分ゲーム完全均衡になります。
◆参考文献

|
 2回繰り返しゲーム
2回繰り返しゲーム 
 2回繰り返しゲーム
2回繰り返しゲーム 