 交渉ゲーム２ |
 |
|
再びアヤカとミカのゲームを考えます。
 VS 
2人はクルマの売り買いをしようとしています。 アヤカのクルマに対してミカは300万円まで払っていいと考えています。 いっぽうアヤカは200万円以上なら売っていいと考えています。 さて2人はいくらで手を打つでしょう。
前回の100ラウンドのモデルでは 2人が共通の割引因子をもつケースを考えました。 今回は同じ100ラウンドのモデルで 2人が異なる割引因子をもつケースを考えます。
前回同様、ミカとアヤカは50回ずつ交互に提示できるとします。 交渉は最大100ラウンドで行なわれます。 交渉の妥結が遅れるたびにコストが発生します。 ただし今回アヤカは性急な女になります。 アヤカは1ラウンド早く交渉がまとまるなら6％の利益減少さえ我慢できるとします。 これはたとえば第100ラウンドで得られる100と 第99ラウンドで得られる94を同等に評価するということです。 ミカは前回同様1ラウンド早く交渉がまとまるなら3％の利益減少を我慢します。 最終第100ラウンドのアヤカの提示から考えます。 100. アヤカが価格P100を提示する。ミカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P100、アヤカの利得はP100-200 。 ミカがこれを拒否した場合、交渉は決裂となり、ゲームは終了する。2人の利得はともに0 アヤカの提示額は300でいいです。このときミカは受け入れるのも拒否するのも無差別 となるので提示を受け入れます。ミカの利得は300-300=0 、アヤカの利得は300-200=100 です。100でのアヤカの最適行動は300を提示することです。 第100ラウンドでどうなるかはわかったので第99ラウンドを考えましょう。 99. ミカが価格P99を提示する。アヤカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P99、アヤカの利得はP99-200 。 アヤカがこれを拒否した場合、ゲームは100へ進む。 第100ラウンドへ進んだ場合のアヤカの利得は100です。 したがって第99ラウンドではアヤカは利得が94以上でなければ受け入れないです。 ミカのP99は294でなければいけません。 99でのミカの最適行動は294を提示することです。 ミカの利得は300-294=6 、アヤカの利得は294-200=94 。 第99ラウンドでどうなるかはわかったので第98ラウンドを考えましょう。 98. アヤカが価格P98を提示する。ミカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P98、アヤカの利得はP98-200 。 ミカがこれを拒否した場合、ゲームは99へ進む。 第99ラウンドへ進んだ場合のミカの利得は6です。 したがって第98ラウンドではミカは利得が6*0.97=5.82以上でなければ受け入れないです。 アヤカのP98は294.18でなければいけません。 98でのアヤカの最適行動は294.18を提示することです。 ミカの利得は300-294.18=5.82 、アヤカの利得は294.18-200=94.18 。 第98ラウンドでどうなるかはわかったので第97ラウンドを考えましょう。 97. ミカが価格P97を提示する。アヤカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P97、アヤカの利得はP97-200 。 アヤカがこれを拒否した場合、ゲームは98へ進む。 第98ラウンドへ進んだ場合のアヤカの利得は94.18です。 したがって第97ラウンドではアヤカは利得が94.18*0.94=88.5292以上でなければ受け入れないです。 ミカのP97は288.5292でなければいけません。 97でのミカの最適行動は288.5292を提示することです。 ミカの利得は300-288.53=11.47 、アヤカの利得は288.53-200=88.53 。 この議論は延々と第1ラウンドまで繰り返していけます。 （各ラウンドと利得の関係は下のようになります。）
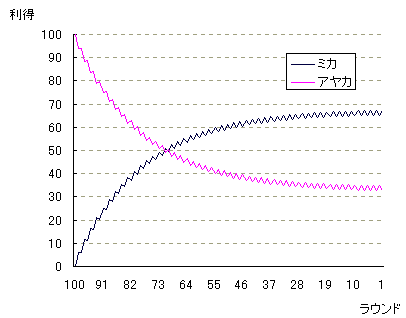
1でのミカの最適行動は232.65の提示だとわかります。 （この数列の計算については下のほうに書きました。） けっきょくゲームは第1段階でミカが232.65を提示し終了します。 ミカの利得は300-232.65=67.35 、アヤカの利得は232.65-200=32.65 です。 パイの分配比はおよそ2：1になります。（これは辛抱強さの比と同じです。） ミカの取り分がずっと増えていることに注目してください。 このモデルは交渉では辛抱強さが大事だということを言っています。
＜数列の計算＞ アヤカの利得に注目します。 アヤカの各ラウンドでの利得は
100R ... 100 と計算していくことができます。 全体のパイの大きさ100万円を1、アヤカの割引因子をa、ミカの割引因子をmとすると アヤカの利得は
100R ... 1 となります。 奇数ラウンド2n-1の利得は偶数ラウンド2nの利得のa倍です。 ラウンド1の利得はラウンド2の利得のa倍です。 ラウンド2の利得は 2R ... 1-m+am-am2+a2m2- … -a48m49+a49m49 です。 したがってラウンド1の利得は 1R ... a-am+a2m-a2m2+a3m2- … -a49m49+a50m49 = A1 です。 A1 = { (a-am)+(a2m-a2m2)+ … +(a49m48-a49m49) } + a50m49 { }の中は初項a-am、公比amの等比数列の第49項までの和なので A1 = {(a-am){1-(am)49}/(1-am)} + a50m49 a=0.94, m=0.97を代入するとA1=0.3265となります。 したがってアヤカの第1ラウンドでの利得は32.65となります。 こうして第1ラウンドでのミカの最適な提示額は232.65とわかります。
◆参考文献
|
