 交渉ゲーム３ |
 |
|
再びアヤカとミカのゲームを考えます。
 VS 
2人はクルマの売り買いをしようとしています。 アヤカのクルマに対してミカは300万円まで払っていいと考えています。 いっぽうアヤカは200万円以上なら売っていいと考えています。 さて2人はいくらで手を打つでしょう。
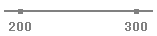
前回・前々回は100ラウンド（有限回ラウンド）のモデルを考えました。 今回は無限回ラウンドのモデルを考えます。
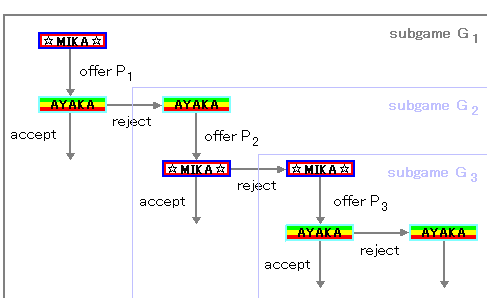
いま次のようなルールで交渉を行なうとしましょう。 1. まずミカが価格P1を提示する。アヤカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P1、アヤカの利得はP1-200 。 アヤカがこれを拒否した場合、ゲームは2へ進む。 2. アヤカが価格P2を提示する。ミカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P2、アヤカの利得はP2-200 。 ミカがこれを拒否した場合、ゲームは3へ進む。 3. ミカが価格P3を提示する。アヤカがこれを受け入れた場合ゲームは終了する。ミカの利得は300-P3、アヤカの利得はP3-200 。 アヤカがこれを拒否した場合、ゲームは4へ進む。 4以下は書かれていませんが、無限に同じことを繰り返します。 どちらかが受け入れるまで続くのです。図にかくと下のようになります。
なお前回同様、アヤカの割引因子を0.94、ミカの割引因子を0.97とします。 つまりアヤカは1ラウンド早く交渉がまとまるなら6％の利益減少さえ我慢できます。たとえば第100ラウンドで得られる100と第99ラウンドで得られる94を同等に評価するということです。ミカは1ラウンド早く交渉がまとまるなら3％の利益減少を我慢します。 さてこのゲームはどういう結果になるでしょう。
これを厳密に考えるのは大変なので とりあえずつぎのように考えます。 もし 第3ラウンドでミカが合理的に提示する額はただ1つしか存在しない としたらどうなるでしょう。 つまり 第3ラウンドに突入したときは ミカもアヤカも先を読んで合理的にある分配 (x, 100-x) で手を打つ ということです。
この場合ゲームはつぎのようになります。 第3ラウンドでミカはxを得ます。 第2ラウンドに戻りましょう。 ミカは自分の取り分がいくらだったら承諾するでしょうか。 これは0.97x万円です。 アヤカは自分の取り分100-0.97x万円を提示します。 第1ラウンドに戻りましょう。 アヤカは自分の取り分がいくらだったら承諾するでしょうか。 これは0.94(100-0.97x)万円です。 ミカは自分の取り分100-0.94(100-0.97x)万円を提示します。 ところが第1ラウンドと第3ラウンドは同じ状況です。 第3ラウンドからのゲームはゲームのやり直しにすぎないからです。 100-0.94(100-0.97x) = x が言えます。 これを解くと
100-94+0.94*0.97x-x = 0 ミカは第1ラウンドで自分の取り分68.03万円を提示します。 このゲームはミカが第1ラウンドで価格231.97万円を提示して 終了します。 次回これをもう少し厳密に考えてみます。
◆参考文献
|
