 交渉ゲーム４ |
 |
|
 VS 
前回の続きです。 アヤカとミカのゲームの無限回ラウンドのモデルです。
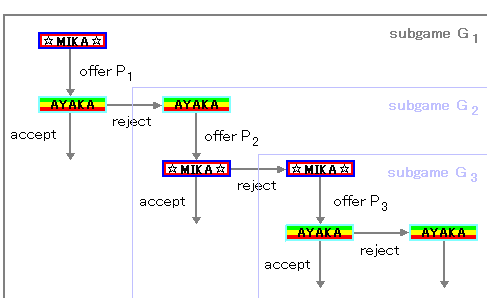
このゲームは ミカの割引因子を0.97、アヤカの割引因子を0.94とすると、 ミカが第1ラウンドで価格231.97万円を提示して終了します。 前回はショートカットを使ってこれを説明しましたが、 今回は少し厳密にこれを説明します。
ミカの立場に立ってみましょう。 ミカにとっての問題は「アヤカに受け入れられる提示額とは何か」 ということです。 これはいいかえれば「部分ゲーム完全となる提示額とは何か」 ということです。 （部分ゲーム完全になっているとは 要は先読みしたときに合理的になっているということです。） 第 3, 5, 7 ... ラウンドと第1ラウンドの状況が変わらないとすると、これは 「第1ラウンドでアヤカに受け入れられる提示額とは何か」 あるいは「部分ゲーム完全となる第1ラウンドでの提示額とは何か」 ということになります。 第1ラウンドでミカがある価格を提示する→アヤカがそれを受け入れるというのが 先を見越したときに合理的になるある価格とは何かということです。 アヤカの立場に立ってみましょう。 アヤカにとっての問題は「（もし自分の提示する番がきたとして）ミカに受け入れられる提示額とは何か」 ということです。 これはいいかえれば「（もし自分の提示する番がきたとして）部分ゲーム完全となる提示額とは何か」 ということです。 第4, 6, 8 ... ラウンドと第2ラウンドの状況が変わらないとすると、 これは「第2ラウンドでミカに受け入れられる提示額とは何か」 あるいは「部分ゲーム完全となる第2ラウンドでの提示額とは何か」 ということになります。 第2ラウンドでアヤカがある価格を提示する→ミカがそれを受け入れるというのが 先を見越したときに合理的になるある価格とは何かということです。 有限回ラウンドの場合はこれを一番最後のラウンドから バックワードインダクションで求めることができましたが 無限回ラウンドの場合はそれができません。 しかし部分ゲーム完全均衡を考えることはできます。
このゲームを考えるためにまず このゲームでは部分ゲームが2種類に分けられることに注目しましょう。 「奇数ラウンドから始まるゲーム」と「偶数ラウンドから始まるゲーム」 の2種類です。 「ミカの提示から始まるゲーム」と「アヤカの提示から始まるゲーム」 の2種類です。 subgame G3 は subgame G1 とまったく同じゲームです。 第3ラウンドの状況は第1ラウンドの状況とまったく同じです。 subgame G4 は subgame G2 とまったく同じゲームです。 第4ラウンドの状況は第2ラウンドの状況とまったく同じです。
さていまG1の部分ゲーム完全均衡（少なくとも1つあると仮定）におけるミカ（Buyer）の最大利得をQB、最小利得をqBとしましょう。 G1 にはいくつか部分ゲーム完全均衡があると仮定して、 それらの均衡におけるミカの利得が最大でQB、最小でqB ということです。 またG2の部分ゲーム完全均衡（少なくとも1つあると仮定）におけるアヤカ（Seller）の最大利得をQS、最小利得をqSとしましょう。 上の2つのパラグラフから、 QBはG3の部分ゲーム完全均衡におけるミカの最大利得、 またqBはG3の部分ゲーム完全均衡におけるミカの最小利得 ということになります。 なお今回利得というのは割合のことです。全体のパイの大きさ100万円を1とします。
QB（G1の部分ゲーム完全均衡におけるミカの最大利得）の上限を考えましょう。 G1の第1ラウンドでミカのオファーがアクセプトされるためには（＝オファーが部分ゲーム完全となるためには）、 アヤカは少なくとも 0.94qSを受け取らないといけません。 （アヤカのG2における最小利得qSの現在価値は0.94qSなので、アクセプトされるためには少なくとも0.94qSでないといけない。） これは同時にミカに多くとも 1-0.94qS しか 残らないことを意味します。 したがってQBは QB ≦ 1-0.94qS ということになります。
同じようにしてqB（G1の部分ゲーム完全均衡におけるミカの最小利得）の下限を考えましょう。 もし第1ラウンドでミカが0.94QS以上をアヤカの取り分として提示したならば アヤカはこれを受け入れます。 （アヤカのG2における最大利得QSの現在価値は0.94QSなので、いま0.94QS以上をもらえればこれを受け入れる。） ミカはアヤカに0.94QSを提示すれば十分です。 ミカには少なくとも 1-0.94QS が残ります。 したがって qBは qB ≧ 1-0.94QS ということになります。
QS（G2の部分ゲーム完全均衡におけるアヤカの最大利得）の上限を考えましょう。 G2の第1ラウンドでアヤカのオファーがアクセプトされる ためには（＝オファーが部分ゲーム完全となるためには）、ミカは少なくとも 0.97qBを受け取らないといけません。 （ミカのG3における最小利得qBの現在価値は 0.97qBなので、アクセプトされるためには少なくとも0.97qBでないといけない。） これは同時にアヤカに多くとも 1-0.97qB しか 残らないことを意味します。 したがってQSは QS ≦ 1-0.97qB ということになります。
同じようにしてqS（G2の部分ゲーム完全均衡におけるアヤカの最小利得）の下限を考えましょう。 もしG2の第1ラウンドでアヤカが0.97QB以上をミカの取り分として提示したならばミカはこれを受け入れます。 （ミカのG3における最大利得QBの現在価値は 0.97QBなので、いま0.97QB以上をもらえればこれを受け入れる。） アヤカはミカに0.97QBを提示すれば十分です。 アヤカには少なくとも 1-0.97QB が残ります。 したがって qSは qS ≧ 1-0.97QB ということになります。
4つの不等式が得られました。 じつはこれら4つの条件からQB、qB、QS、qS の値を突き止めることができます。
としましょう。 まずQBから考えます。 (iv)の両辺に-0.94（＜0）を掛けます。 -0.94qS ≦ -0.94(1-0.97QB) これに1を加えます。 1-0.94qS ≦ 1-0.94(1-0.97QB) 1-0.94qS ≦ 1-0.94+0.94*0.97QB ・・・ (v) (i)と(v)より QB ≦ 1-0.94+0.94*0.97QB ・・・ (vi) これを変形すると QB-0.94*0.97QB ≦ 1-0.94 QB(1-0.94*0.97) ≦ 1-0.94 QB ≦ (1-0.94)/(1-0.94*0.97) ・・・ (vii)
同様にしてqBを考えます。 (iii)の両辺に-0.94（＜0）を掛けます。 -0.94QS ≧ -0.94(1-0.97qB) これに1を加えます。 1-0.94QS ≧ 1-0.94(1-0.97qB) 1-0.94QS ≧ 1-0.94+0.94*0.97qB ・・・ (viii) (ii)と(viii)より qB ≧ 1-0.94+0.94*0.97qB これを変形すると qB-0.94*0.97qB ≧ 1-0.94 qB(1-0.94*0.97) ≧ 1-0.94 qB ≧ (1-0.94)/(1-0.94*0.97) ・・・ (ix)
整理すると
この2つの不等式を合わせると
ところが定義により
(x), (xi) より
となります。
QS, qSについてはBとS、また0.94と0.97を入れ換えて
となります。
(xii)は G1の部分ゲーム完全均衡におけるミカの利得が一意に決まることを示しています。第1ラウンドで自分の取り分としてたった1つだけ合理的に提示できるのが(1-0.94)/(1-0.94*0.97)ということです。 ミカは第1ラウンドで100*(1-0.94)/(1-0.94*0.97)=68.03万円を提示します。 つまり価格231.97万円を提示します。アヤカはこれを受け入れます。 このゲームはただ1つの部分ゲーム完全均衡をもちます。
一般には ミカの割引因子0.97をδB, アヤカの割引因子0.94をδSにおきかえればよいので つぎのようになります。
(xiii)は G1の部分ゲーム完全均衡におけるミカの利得が一意に決まることを示しています。第1ラウンドで自分の取り分としてたった1つだけ合理的に提示できるのが (1-δS)/(1-δBδS) ということです。 ミカは第1ラウンドで100*(1-δS)/(1-δBδS)万円を提示します。 つまり価格300-100*(1-δS)/(1-δBδS)万円を提示します。アヤカはこれを受け入れます。 ゲームはただ1つの部分ゲーム完全均衡をもちます。
これは強力な結果ですのでおぼえておく価値があるとおもいます。
上の命題をグラフにすると下のようになります。
相手の割引因子を所与としたとき自分の割引因子が大きいほど利得は大きくなる。
◆参考文献
|
