 オークション３ |
 |
リカとマリが再びお宝チケットのオークションで争っています。 オークションの参加者はこの2人だけです。
 VS 
今回は前回、前々回とちがってリカもマリも相手の評価額を正確には知りません。 リカとマリは相手の評価額は0-10万円の間でどれも等しくありうると考えています。 たとえばリカの評価額が0-25,000円の間にある確率は1/4です。 （ふと時計に目をやったときに秒針が北東(12-3)を指している確率は1/4 とふつう考えますがそれと同じです。） このオークションは封印入札方式で、一番高い入札をしたプレーヤーが落札するというルールです。つまり封筒に価格を書いた紙を入れ、それを主催者に渡します。そして高い価格をつけていたほうが落札します。入札の単位は1円単位までOKで、60,001円とかいうのもありです。 さて、このオークションはどういう結果になるでしょう。なお細かくビッドできるので2人は同じ価格をつけることはないとします。
たとえばリカの評価額が6万円であるとしましょう。 リカはどうするでしょうか。 完全ポジティブモードなら1円を入札すべきです。 余剰59,999円を思い切って狙いにいくのです。 完全ネガティブモードなら59,999円を入札すべきです。 余剰1円をせこく取りにいくのです。 ・・・前者はあまりにも無謀で、後者はおもしろくありません。 答えは中間にあるとおもいます。 リカは55,000円とか50,000円とか、 適当に6万円から割り引いた額を入札するはずです。 結論から先に言います。 いま自分の評価額（＝自分のタイプ）がどんなものであっても、 いつもその半分だけを入札額にすることを「半分ルール」ということにしましょう。 するとこのゲームではお互いこの「半分ルール」をとることがナッシュ均衡（ベイズ・ナッシュ均衡）になるのです。
確認してみましょう。 試しにリカの評価額が6万円であった場合を考えます。リカは
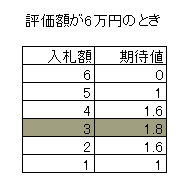
1. マリの評価額は0-10万円の間でどれも等しくありうると考えています。 リカはいくら入札すべきでしょう。 5万円をつけると（3の仮定のもとでは）必ず勝つことができて、このとき1万円の余剰を得ます。 5万円がベストでしょうか？ 4万円をつけるとします。 マリの入札額が4万円以下になる確率は4/5=0.8です。（3の仮定のもとではリカはそう考えます。） したがって落札する確率は0.8とリカは考えます。 落札しない確率は0.2です。 期待値は (6-4)*0.8+0*0.2 = 2*0.8 = 1.6 (万円)になります。 3万円をつけるとします。 マリの入札額が3万円以下になる確率は3/5=0.6です。 したがって落札する確率は0.6です。 落札しない確率は0.4です。 期待値は (6-3)*0.6+0*0.4 = 3*0.6 = 1.8 (万円)になります。 2万円をつけるとします。 マリの入札額が2万円以下になる確率は2/5=0.4です。 したがって落札する確率は0.4です。 落札しない確率は0.6です。 期待値は (6-2)*0.4+0*0.6 = 4*0.4 = 1.6 (万円)になります。 どうも3万円ぐらいをつけるのがいいみたいです。 リカの割引率をk1（0＜k1＜1）とします。 つまりリカは評価額6万円にk1を掛けたものを入札するとします。 リカの入札額は6k1万円です。 マリの入札額が6k1万円以下になる確率は6k1/5です。 （いまリカは5万円未満を入札するならどうするかということを考えているので0＜6k1＜5です。） リカの期待値は
(6-6k1)*(6k1/5) + 0*(1-(6k1/5))
になります。この2次関数は上に凸で 横軸と0, 1で交わります。対称性から最大値をとるのはk1=0.5のときです。 （下図。）
3万円がベストです。 こうして リカは評価額が6万円の場合、マリが半分ルールを使うと仮定すると、 その半分を書くのが最適であることがわかりました。
リカの評価額が8万円である場合はどうでしょう。 マリが半分ルールを使うという仮定のもとでは、 マリの入札額は0-5万円の範囲なので、 リカは5万円をつければ勝てます。期待値は3万円です。 リカの割引率をk1とします。 リカの入札額は8k1万円です。 マリの入札額が8k1万円以下になる確率は8k1/5です。 （いまリカは5万円未満を入札するならどうするかということを考えているので0＜8k1＜5です。） リカの期待値は
(8-8k1)*(8k1/5) + 0*(1-(8k1/5))
やはり半分を書くのが最適です。 期待値は(64/5)(1/2)(1/2)=64/20=16/5=3.2万円となります。
リカの評価額が4万円である場合はどうでしょう。 まずリカの入札額は4万円以下でなければ意味がないです。
マリの入札額は0-5万円で等しくありえます。
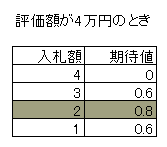
4万円をつけると落札できる確率は4/5です。
3万円をつけると落札できる確率は3/5です。
2万円をつけると落札できる確率は2/5です。
1万円をつけると落札できる確率は1/5です。 2万円ぐらいがベストみたいです。 リカの入札額は4k1万円です。 マリの入札額が4k1万円以下になる確率は4k1/5です。 リカの期待値は
(4-4k1)*(4k1/5) + 0*(1-(4k1/5))
やはり半分を書くのが最適です。
リカの評価額をV1とします。 リカはマリの評価額は0-10万円の間でどれも等しくありうると考えています。 リカはマリが半分ルールを使うと仮定します。 リカはマリの入札額は0-5万円の間でどれも等しくありうると考えます。 1. 評価額V1が5万円以上10万円以下のとき リカは
(1) 5万円を書くか で迷います。
(1)の期待値は V1-5 万円です。 リカの割引率をk1 (0＜k1＜1)とします。 リカの入札額はV1k1万円です。 ここで0＜V1k1＜5です。 マリの入札額がV1k1万円以下になる確率は V1k1/5です。 リカが落札する確率はV1k1/5です。 リカの期待値は
(V1-V1k1)*(V1k1/5) + 0*(1-(V1k1/5))
になります。 k1=1/2 のとき最大値 (V12/5)(1/2)(1/2)=V12/20 をとります。 (1)と(2)はどっちがいいでしょう。 V1-5 と V12/20 を比較します。
(V1-5) - (V12/20) より V1-5 ≦ V12/20 です。 つねに(2)のほうがいいです。リカは5万円未満ただし評価額のちょうど半分を書くのが最適です。 2. 評価額が0万円以上5万円未満のときは 5万円未満でどうするかが問題なので1の(2)と同じです。半分を書くのが最適です。 こうしてリカは、マリが半分ルールを使うと仮定すると、 自分の評価額がいくらであっても、半分を書くのが最適であることがわかります。 つまり半分ルールを使うことが最適です。
マリについても同じ議論ができます。 マリは、リカが半分ルールを使うと仮定すると、 自分の評価額がいくらであっても、半分を書くのが最適であることがわかります。 つまり半分ルールを使うことが最適です。 いまマリの半分ルールを前提とするとリカは半分ルールが最適です。 逆にリカの半分ルールを前提とするとマリは半分ルールが最適です。 互いに半分ルールを使うというのはナッシュ均衡（ベイズ・ナッシュ均衡）です。
◆参考文献
|
