 オークション４ |
 |
再びお宝チケットのオークションを考えます。 前回の「オークション３」で参加者がもう１人増えたらどうなるでしょう。 ケイが参戦するとします。
  
どの参加者も他の参加者の評価額を正確には知りません。 他の参加者の評価額は0-10万円の間でどれも等しくありうると考えています。 さて、このオークションはどういう結果になるでしょう。なお細かくビッドできるので3人は同じ価格をつけることはないとします。
結論から先に言います。 いま自分の評価額（＝自分のタイプ）がどんなものであっても、 いつもその2/3だけを入札額にすることを「2/3ルール」ということにしましょう。 するとこのゲームでは3人ともこの「2/3ルール」をとることがナッシュ均衡（ベイズ・ナッシュ均衡）になるのです。
確認してみましょう。 試しにリカの評価額が6万円であった場合を考えます。リカは
1. マリ・ケイの評価額はそれぞれ0-10万円の間でどれも等しくありうると考えています。 リカはいくら入札すべきでしょう。まず6万円以下でなければ意味がないです。 6万円。勝ったとしても余剰は0です。 5万円。マリの入札額が5万円以下になる確率は5/(20/3)=15/20=3/4です。 ケイの入札額が5万円以下になる確率も3/4です。 したがってリカが落札する確率は(3/4)(3/4)=9/16です。 リカが落札しない確率は7/16です。 リカの期待値は (6-5)*(9/16)+0*(7/16)=9/16=0.56 (万円)になります。 4万円。マリの入札額が4万円以下になる確率は4/(20/3)=12/20=3/5です。 ケイの入札額が4万円以下になる確率も3/5です。 したがってリカが落札する確率は(3/5)(3/5)=9/25です。 リカが落札しない確率は16/25です。 リカの期待値は (6-4)*(9/25)+0*(16/25)=18/25=0.72 (万円)になります。 3万円。マリの入札額が3万円以下になる確率は3/(20/3)=9/20です。 ケイの入札額が3万円以下になる確率も9/20です。 したがってリカが落札する確率は(9/20)(9/20)=81/400です。 リカが落札しない確率は319/400です。 リカの期待値は (6-3)*(81/400)+0*(319/400)=243/400=0.61 (万円)になります。 どうも4万円ぐらいをつけるのがいいみたいです。 リカの割引率をk1 (0＜k1＜1) とします。 リカの入札額は6k1万円です。 マリの入札額が6k1万円以下になる確率は6k1/(20/3)=18k1/20=9k1/10です。 （ここで0＜6k1＜6＜20/3です。） ケイの入札額が6k1万円以下になる確率も9k1/10です。 リカが落札する確率は(9k1/10)2です。 リカの期待値は
(6-6k1)*(9k1/10)2+0*{1-(9k1/10)2}
です。あらためて f(k1) = (1-k1)k12 とおいてこれが最大値をとるときのk1を求めます。 f(k1) = -k13+k12 微分して f '(k1) = -3k12+2k1 = -3k1(k1-(2/3)) 0＜k1＜1に注意します。 f '(k1) は接線の傾きを表します。 k1=0.5における接線の傾きは正です。 k1=0.8における接線の傾きは負です。 k1=2/3における接線の傾きは0です。 したがって f(k1) は最初は増加（上り）、k1=2/3で極大（頂上）、あとは減少（下り）になります。（下図。） f(k1) が最大値をとるのはk1=2/3のときです。
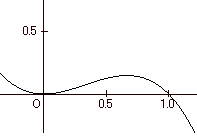
4万円がベストです。 こうして リカは評価額が6万円の場合、マリ・ケイが2/3ルールを使うと仮定すると、 2/3を書くのが最適であることがわかりました。
リカの評価額が8万円である場合はどうでしょう。 マリ・ケイが2/3ルールを使うという仮定のもとでは、 マリ・ケイの入札額は0-6.67万円の範囲なので、 リカは6.67万円をつければ勝てます。期待値は1.33万円です。
リカの割引率をk1とします。 リカの入札額は8k1万円です。 マリの入札額が8k1万円以下になる確率は8k1/(20/3) =24k1/20=6k1/5です。 （いまリカは6.67万円未満を入札するならどうするかということを考えているので0＜8k1＜20/3です。） ケイの入札額が8k1万円以下になる確率も6k1/5です。 リカが落札する確率は(6k1/5)2です。 リカの期待値は
(8-8k1)*(6k1/5)2 + 0*{1-(6k1/5)2}
やはり2/3を書くのが最適です。 期待値は(288/25)(1/3)(2/3)2=(288/25)(4/27)=1152/675=1.71万円となります。
リカの評価額が4万円である場合はどうでしょう。 マリの入札額は0-6.67万円で等しくありえます。 ケイの入札額も0-6.67万円で等しくありえます。 リカの入札額は4万円以下でなければ意味がないです。 4万円。勝ったとしても余剰は0です。
3万円をつけると落札できる確率は{3/(20/3)}2です。
2万円をつけると落札できる確率は{2/(20/3)}2です。
1万円をつけると落札できる確率は{1/(20/3)}2です。
リカの入札額は4k1万円です。 マリの入札額が4k1万円以下になる確率は4k1/(20/3)=12k1/20=3k1/5です。 ケイの入札額が4k1万円以下になる確率も3k1/5です。 リカが落札する確率は(3k1/5)2です。 リカの期待値は
(4-4k1)*(3k1/5)2 + 0*(1-(3k1/5)2)
やはり2/3を書くのが最適です。 リカは 4(2/3)=8/3=2.67万円を入札し、 そのときの期待値は(36/25)(1/3)(2/3)2=(36/25)(4/27)=144/675=0.21万円です。
リカの評価額をV1とします。 リカはマリ・ケイの評価額がそれぞれ0-10万円の間でどれも等しくありうると考えています。 リカはマリ・ケイが2/3ルールを使うと仮定します。 リカはマリ・ケイの入札額がそれぞれ0-6.67万円の間でどれも等しくありうると考えます。 1. 評価額V1が6.67万円以上10万円以下のとき リカは
(1) 6.67万円を書くか で迷います。
(1)の期待値は V1-(20/3) 万円です。 リカの割引率をk1 (0＜k1＜1) とします。 リカの入札額はV1k1万円です。 ここで0＜V1k1＜20/3です。 マリの入札額がV1k1万円以下になる確率は V1k1/(20/3)です。 ケイの入札額がV1k1万円以下になる確率も V1k1/(20/3)です。 リカが落札する確率は{V1k1/(20/3)}2です。 リカの期待値は
(V1-V1k1)*{V1k1/(20/3)}2 + 0*(1-{V1k1/(20/3)}2)
になります。 k1=2/3 のとき最大値
(V13)(1/3)(2/3)2/(20/3)2 をとります。 (1)と(2)はどっちがいいでしょう。 V1-(20/3) と V13/300 を比較します。
{V1-(20/3)} - (V13/300)
= -(1/300) (V1-10) (V12+10V1-200)
6.67≦V1≦10より 上式≦0です。 V1-(20/3) ≦ V13/300 です。 つねに(2)のほうがいいです。リカは6.67万円未満ただし評価額のちょうど2/3を書くのが最適です。 2. 評価額が0万円以上6.67万円未満のときは 6.67万円未満でどうするかが問題なので1の(2)と同じです。2/3を書くのが最適です。 こうしてリカは、マリ・ケイが2/3ルールを使うと仮定すると、 自分の評価額がいくらであっても、2/3を書くのが最適であることがわかります。 つまり2/3ルールを使うことが最適です。
マリについても同じ議論ができます。 マリはケイ・リカが2/3ルールを使うと仮定すると、 自分の評価額がいくらであっても、2/3を書くのが最適であることがわかります。 ケイについても同じ議論ができます。 ケイはリカ・マリが2/3ルールを使うと仮定すると、 自分の評価額がいくらであっても、2/3を書くのが最適であることがわかります。 いま他の2人の2/3ルールを前提とするとプレーヤーは2/3ルールが最適です。 3人が2/3ルールを使うというのはナッシュ均衡（ベイズ・ナッシュ均衡）です。
一般に参加者がn人のときはどうなるでしょう。 いまリカの評価額を V1 、割引率を k1 、 第nプレーヤーの割引率をknとします。
参加者が2人のとき： 参加者が3人のとき： たぶん4人のときは k1=3/4 、5人のときは k1=4/5 が最適になるでしょう。
参加者が4人のとき： 参加者が5人のとき： 一般に参加者がn人のとき、 リカの他のプレーヤーたちが (n-1)/n ルールを使うと仮定すると、 リカの期待値は V1n(1-k1)k1n-1/(10n-1k2k3...kn) になります。式の真ん中の部分 (1-k1)k1n-1 をあらためて f(k1) = -k1n+k1n-1 とおいて微分します。
f '(k1) = -nk1n-1+(n-1)k1n-2
k1 = (n-1)/n のとき最適になります。
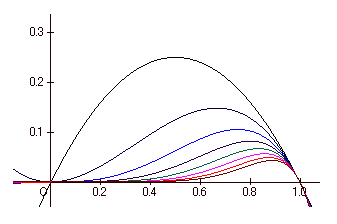
他のプレーヤーについても同様の議論ができます。 あるプレーヤーは他のプレーヤーたちが (n-1)/n ルールを使うと仮定すると、 自分の評価額がいくらであっても (n-1)/n を書くのが最適です。 いま他の n-1 人の (n-1)/n ルールを前提とするとプレーヤーは (n-1)/n ルールが最適です。 n人が (n-1)/n ルールを使うというのはナッシュ均衡（ベイズ・ナッシュ均衡）です。
◆参考文献
|
