ベイズのケーキ

モームス女子大学、学生ラウンジ。ある金曜日の午後です。 仲良しコンビのアイとノノがオリジナルの歌とダンス の研究をしていました。 向上心あふれる２人です。そこに出張帰りの中澤教授が現れました。「ケーキ買ってきたぜベイビー」。 どうやらパチンコで勝ったようです。 モームス市でケーキといえばそれはベイズ屋のケーキです。 もちろんアイとノノは筋金入りの「ベイジアン」です。 さてどうしたことか外見がまったく同じ箱が２つあります。何かイヤな予感がします。 　＜　はい、差し入れ２択クイズです。片方の箱にはチョコレートケーキと イチゴのショートケーキが３個ずつ入っています。 もう片方の箱にはチョコが１個とイチゴが３個入っています。 あなたたちでどっちか１つの箱を選んでください。 もちろんアイとノノにとっては６個入った箱のほうがいいです。 しかしこれは 50：50 の賭けです。 　＜　でも今日はサービスです。 どっちかの箱からケーキを１個だけとってみていいです。 それを参考にしてまた考えてください。 ２人が片方の箱から１個とってみるとチョコが出ました。 　＜　チョコが出たってことは、この箱が当たりの確率が高いで。 　＜　そうれす。当たりの箱は 1/2 の高確率でチョコが出るれす。ハズレの箱は 1/4 の低確率れす。 つまり２：１でこっちが有利れす。この箱を選ぶのが合理的れす。 ケーキを目の前にして、ノノの様子がいつもと違います。 さて、情報を与えられたことでアイとノノが認識を改めるのは当然です。 まず、サンプルを見る前は、サンプルが当たり箱のものである確率は 1/2 と考えるしかないです。 しかしサンプルを見たあとでは、 この確率を修正してもいいはずです。 ではどう修正するのが妥当でしょう。 それには条件つき確率（別項参照）を考えます。 すなわち サンプルがチョコであるという条件のもとで サンプルが当たり箱のものである確率 を 考えるのです。 いま サンプルが A：当たり箱のものである B：チョコレートケーキである C：ハズレ箱のものである とします。すると、条件つき確率を考えて P(A) = 1/2 PA(B) = 1/2 PC(B) = 1/4 P(C) = 1/2 です。そして求める確率は 　PB(A)　です。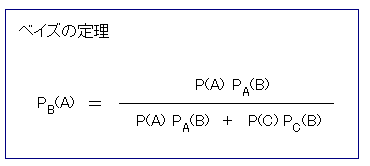これは より 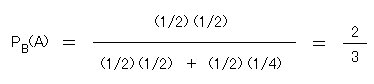です。 図でかくと下のようになります。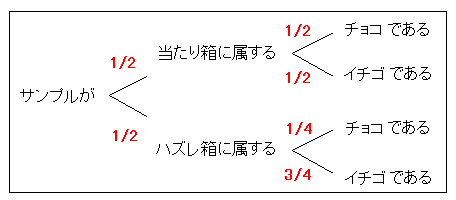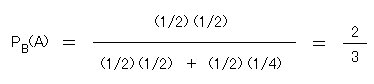 サンプルがチョコであるという条件のもとで、サンプルが当たり箱のものである確率は サンプルをとったあとで、このゲームで考えるべき確率が変わりました。 サンプルをとるまえに考えた確率を事前確率、 サンプルをとったあとで考えた確率を事後確率といいます。アイとノノは情報を与えられて 事前確率を事後確率に更新しました。 ベイズの定理は条件つき確率の定義から導かれます。（別項参照） P(A)=P(C)=1/2 の場合は分子分母が 1/2 で割れるので実際は ノノが計算したように PB(A)=0.5/(0.5+0.25)=2/(2+1)=2/3 とやればよいです。 サンプルがイチゴだった場合は、この箱が当たり箱である確率は 0.5/(0.5+0.75)=2/(2+3)=2/5 です。もう一方の箱が当たりである確率が 3/5 なので、こっちに賭けます。 このゲームから ＜情報とは不確実性を減らすもの＞と定義できることがわかります。 ◆参考文献 『＜不確実性と情報＞入門』　 　 金子郁容、岩波書店、1990年 『基本統計学』　 　 宮川公男、有斐閣、1999年 『ゲームと情報の経済分析』　 エリック・ラスムセン、九州大学出版会、1990年　 GAMES AND INFORMATION : AN INTRODUCTION TO GAME THEORY (1989)