 情報の価値 |
 |
|
そういえば前回の「ベイズのケーキ」で中澤教授が
サンプルをとることを許可する際に
「今日はサービスです」と言っていました。
たしかにふつう情報を手に入れるにはコストがかかります。
いまベイズのケーキの当たり箱がアイとノノにとって3000円の価値があり、 ハズレの箱は2100円の価値があるとしましょう。 このとき本来、アイとノノは中澤教授に情報の対価としていくら払うべきなのでしょうか。
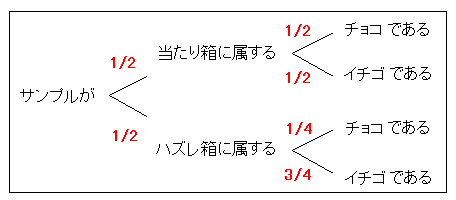
 これを考えるためには、ゲームの期待値を ＜情報がなかった場合＞と＜情報があった場合＞について考えればよいです。 ◆情報がなかった場合。 この場合は E = (1/2)*3000+(1/2)*(2100) = 1500+1050 = 2550 （円） です。つまりゲームの期待値は2550円です。 ◆情報があった場合。つまりサンプルをとってよい場合です。 まずサンプルはチョコかイチゴなのでこの２通りで場合分けができます。
◆これらに
それぞれが起こる確率を掛けて加重平均をとれば
サンプルをとった場合の期待値が求められます。
サンプルがチョコである確率は図より
したがって求める期待値は E = (3/8)(2700) + (5/8)(2640) = (8100/8)+(13200/8) = 21300/8 = 2662.5 （円） です。 ◆以上より、サンプルをとらなかった場合の期待値が2550円、 サンプルをとった場合の期待値が2662.5円なので、 このゲームで中澤教授がくれた情報の価値は112.5円と考えられます。 したがって本来アイとノノは中澤教授に112．5円を払うべきであると考えられます。
（補足） ◆サンプルがチョコである確率は P(B) です。そして P(B) = PA(B)P(A) + PC(B)P(C) これは条件つき確率の定義式からベイズの定理を導く過程で 出てきます。 ベイズの定理の証明
◆参考文献
|
