チャーミーの挑戦２

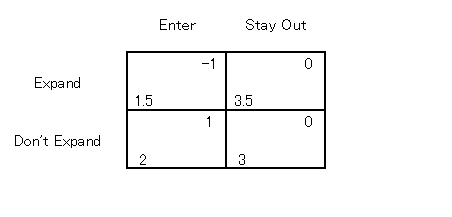
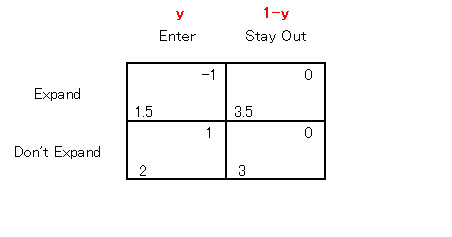
前回の「チャーミーの挑戦」の設定を少しだけ変えてみましょう。セクシーのプラント拡大のコストを1.5億（高い場合）またはゼロ（低い場合）としてみるのです。 セクシー VS チャーミー プレーヤーの利得は下のテーブルで表されます。 コストが高い場合 コストが低い場合 このゲームはどういう結果になるでしょう。 これはかなりやっかいです。というのは、コストが高い場合はセクシーの Don't Expand はいぜん支配戦略ですが、コストが低い場合の Expand が支配戦略でなくなっているのです。 そういうわけで、コストが低い場合のセクシーの最適戦略というのは、チャーミーの戦略によって変わってきます。つまり、チャーミーは確率 y で参入してくるだろうと、セクシーが考えたとします。 コストが低い場合 すると、 拡大するときの期待値　1.5y + 3.5(1-y) = 3.5-2y 拡大しないときの期待値　2y + 3(1-y) = 3-y となって、 3.5-2y > 3-y or y < 1/2 のとき拡大し、 y > 1/2 のとき拡大しないことになります。 このように、セクシーの最適戦略は、チャーミーの戦略によって変わってきます。 ところがいっぽう、そのチャーミーの戦略は、セクシーの戦略はもちろん、先に見たように p1 の値によっても変わってきます。大変ややこしい状況です。 ◆ゲームの変換 ゲーム理論では、こういう複雑な状況を扱うために、ゲームの変換を考えます。 このゲームのポイントは、セクシーはプラント拡大のコストについて知っているけれども、チャーミーはそれを知らないという情報の非対称性です。 いま、これをつぎのように考えてみます。 まず、セクシーも自分のコストについて知らないというところまで 時間を戻してみます。コストについて調査中という時点ですね。 そうすると、セクシーの戦略というのは、もしコストが高かったらどうする、 もしコストが低かったらどうする、という計画になるとおもいます。 赤ちゃんが生まれる前のお母さんが、もし男の子だったらどうする、 もし女の子だったらどうする、という青写真を描くみたいなかんじですね。 さて、セクシーも何もわからないという段階では、コストがどうなるかということは運次第（確率の問題）であり、いいかえれば自然というプレーヤーの選択いかんということです。そして、セクシーにとって、調査結果がわかるということは、いいかえれば自然の選択をみることができるということです。 そこでゲームは、まず自然というプレーヤーが動いて、そのあとにセクシーが動くゲームと考えることができます。これはつぎのようなツリーでかけます。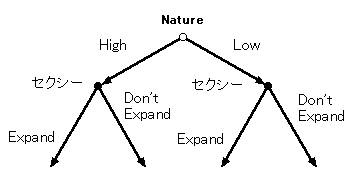 お母さんはじっさいに赤ちゃんが生まれて、性別を確認したあとに行動をとることができるので、お母さんの意思決定点は２つかくことになります。 セクシーも調査結果をみて、行動をとることができます。 自然がセクシーのコストが高いか低いかというセクシーの「タイプ」を選び、 セクシーはそれを確認したあとに行動をとることができます。 セクシーの戦略は４つあることがわかります（たとえば Don't Expand - Expand など）。左の点と右の点での組合せですね。 （→「ナッシュ均衡３」の戦略の考え方です。） さて、つぎにチャーミーについて考えます。チャーミーはとうぜん、 調査結果をみることができません。これは、セクシーと違って、自然の選択をみることができないということです。そして、セクシーの行動をみることもできません。 そこで、ゲームの続きは下のようにかけるとおもいます。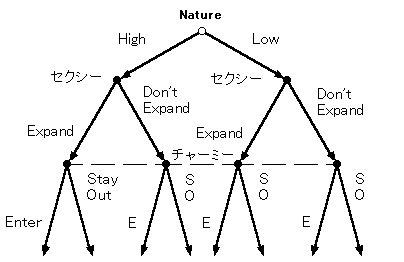 チャーミーは４つの点のうち、どこにいるかわからないので、線で結んでいます。 チャーミーの戦略は Enter か Stay Out の２つです。 さて、いまチャーミーは、自然が High を選ぶ確率を p1 、 Low を選ぶ確率を 1-p1 と考えるとします。そして、やや強引な仮定かもしれませんが、 セクシーも自然が動く前の状態ではチャーミーとかわらないので、セクシーも自然が High を選ぶ確率を p1 、 Low を選ぶ確率を 1-p1 と考えるとします。２人とも共通の事前確率分布を考えるということです。 最後に、利得を書き込んで、ゲームツリーが完成します。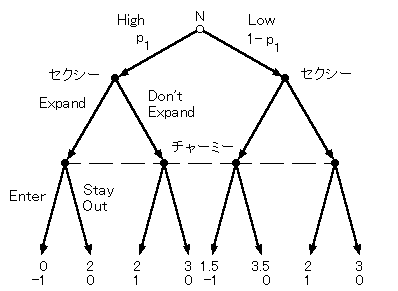 けっきょく、自然という新しいプレーヤーを導入して、２人の情報の非対称性を、自然の選択が観察できるかどうかということに 置き換えてみたわけです。どこかぎこちないかもしれませんが、このようにゲームを捉えなおすことで、今までどおりゲームを考えることができます。 ◆ベイズ・ナッシュ均衡 このように変換されたゲームをベイジアンゲームといいます。 いま、セクシーがコストが低い場合にプラントを拡大する確率を x としましょう。 （コストが高い場合はけっして拡大しません。） そして、チャーミーが参入する確率を y とします。 そこで、つぎのような (x, y) の組を探してみます。すなわち (1)　x は Low タイプにおける最適反応 (2) 見積もり確率 p1 のとき、チャーミーの y は最適反応 いま、たとえば p1 = 0.8 としましょう。事前の段階で、チャーミーはいろんな情報を総合して、どうも高確率でセクシーは High タイプらしいと見積もったとします。 コストが高い場合　0.8 コストが低い場合　0.2 そして、 (x, y) = (0, 1) としてみます。セクシー（ Low タイプ）は拡大せず、チャーミーは参入するという戦略の組合せですね。するとこれは上の条件をみたしていることがわかります。すなわち、チャーミーが参入するというのを前提にしたとき、セクシー（ Low タイプ）が拡大しないのは最適反応です。いっぽう、セクシー（ Low タイプ）が拡大しないのを前提としたとき、チャーミーは参入するのが最適反応です。なぜなら、 p1 = 0.8 とすると、 Enter のときの期待値は 1*0.8 + 1*0.2 = 1 、 Stay Out のときの期待値は 0 だからです。じっさい、どんな p1 でも 1p1 + 1(1-p1) ≧ 0 は成り立つので、 p1 の値にかかわらず、 (x, y) = (0, 1) は上の条件をみたします。 さて、この (x, y) = (0, 1) は、「互いに最適反応」という、今までのナッシュ均衡の概念をそのまま当てはめたものです。ベイジアンゲームのナッシュ均衡をとくにベイズ・ナッシュ均衡といいます。 より正確には、 High タイプでの行動と合わせて、 p1 の値にかかわらず (セクシー, チャーミー) =（ Don't Expand - Don't Expand , Enter） は ベイズ・ナッシュ均衡 ということになります。 ◆他の均衡 p1 = 0.2 としてみましょう。どうもセクシーは高確率で Low タイプらしいという見込みですね。すると (x, y) = (1, 0) はベイズ・ナッシュ均衡になります。すなわちセクシー（ Low タイプ）は拡大し、チャーミーは参入しないという戦略の組です。 コストが高い場合　0.2 コストが低い場合　0.8 いま、チャーミーの Stay Out を前提とすると、Lowセクシーは Expand が最適反応です。 逆に、Lowセクシーの Expand を前提とすると、チャーミーが Enter のときの期待値は 1*0.2 + (-1)*0.8 = -0.6 、 Stay Out のときの期待値は 0 です。 したがってチャーミーの Stay Out は最適反応になります。 じっさい、 1p1 + (-1)(1-p1) ≦ 0 、すなわち p1 ≦ 1/2 ならばいつでも (x, y) = (1, 0) はベイズ・ナッシュ均衡になります。 より正確には、 High タイプでの行動と合わせて、 p1 ≦ 1/2 ならば (セクシー, チャーミー) =（ Don't Expand - Expand , Stay Out） は ベイズ・ナッシュ均衡 ということになります。 ◆参考文献 GAME THEORY　 Drew Fudenberg, Jean Tirole, MIT Press, 1991