 男と女２ |
 |
|
前回の続きです。
問題をよりいっそう複雑にしてみましょう。
今回は女のタイプが2種類あるだけでなく、男のタイプも2種類あるとするのです。
男には Pessimist (タイプ1) と Optimist (タイプ2) の2種類があります。 Pessimistは女が自分を愛してくれている(Loving)とはあんまり思わないです。 Lovingの確率は低い（ρL）と考えます。 いっぽうOptimistはLovingの確率は高い（ρH）と考えます。 またプレーヤーたちは事前確率として Pessimistの存在率を q 、Optimistの存在率を 1-q と考えます。 前回同様、タイプ i の女の戦略を μi とします。 μi はFを選ぶ確率です。 つまりタイプ1の女の戦略はμ1です。 μ1はFを選ぶ確率です。 タイプ2の女の戦略はμ2です。 μ2はFを選ぶ確率です。 したがって女の戦略はμ1とμ2の組み合わせになります。 女の戦略は (μ1, μ2) です。 同じようにタイプ j の男の戦略を λj とします。 λj はFを選ぶ確率です。 つまりタイプ1の男の戦略はλ1です。 λ1はFを選ぶ確率です。 タイプ2の男の戦略はλ2です。 λ2はFを選ぶ確率です。 したがって男の戦略はλ1とλ2の組み合わせになります。 男の戦略は (λ1, λ2) です。 そこでこのゲームのベイズ・ナッシュ均衡は 各プレーヤーの各タイプが最適反応をしているような (λ1, λ2, μ1, μ2) の組み合わせ になります。
純粋戦略の範囲でベイズ・ナッシュ均衡を求めてみましょう。 まず男が両方のタイプでFを選ぶような均衡があるかどうかを調べます。 いま男が両方のタイプでFを選ぶと仮定すると、 タイプ1(Loving)の女の最適反応はF、 タイプ2(Leaving)の最適反応はOになります。 逆に女が(F, O)をプレイすると仮定しましょう。 男が各タイプでFをプレイするのは最適反応でしょうか。 Pessimist（タイプ1）について考えてみましょう。 彼は女がLovingである確率をρLと考えます。
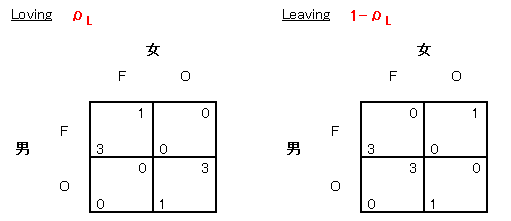
女の (F, O) を前提とすると、彼は F をプレイすることによって期待利得 3ρL + 0(1-ρL) = 3ρL を得ます。 O をプレイすることによって期待利得 0ρL + 1(1-ρL) = 1-ρL を得ます。 したがって 3ρL ≧ 1-ρL 、すなわち ρL ≧ 1/4 ならば F は彼の最適反応になります。
Optimist（タイプ2）について考えてみましょう。 彼は女がLovingである確率をρHと考えます。
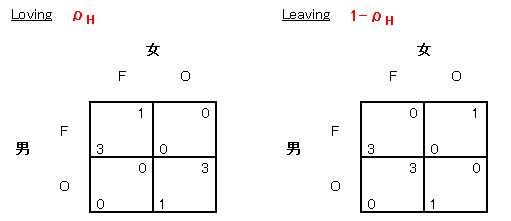
女の (F, O) を前提とすると、彼は F をプレイすることによって期待利得 3ρH + 0(1-ρH) = 3ρH を得ます。 O をプレイすることによって期待利得 0ρH + 1(1-ρH) = 1-ρH を得ます。 したがって 3ρH ≧ 1-ρH 、すなわち ρH ≧ 1/4 ならば F は彼の最適反応になります。 いまρL≧1/4としましょう。 ρH＞ρL（定義）なのでρH＞1/4です。 このとき女の (F, O) に対するFは両方のタイプの男にとって最適反応となります。 逆に男の (F, F) に対しては女の (F, O) は最適反応です。 ρL≧1/4のとき (λ1, λ2, μ1, μ2) = (1, 1, 1, 0) はベイズ・ナッシュ均衡になります。（qの値には関係ありません。）
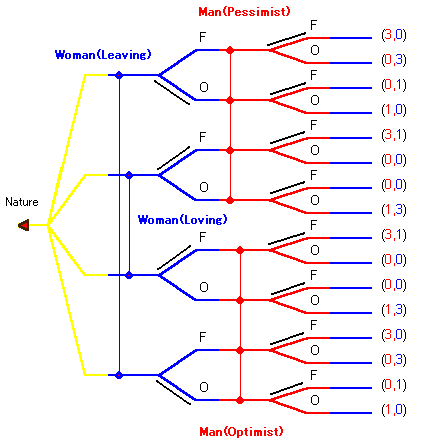
ベイズ・ナッシュ均衡（純粋戦略）は他にもあります。 ρL≧3/4のとき (λ1, λ2, μ1, μ2) = (0, 0, 0, 1) はベイズ・ナッシュ均衡になります。 qの値には関係ありません。 確認してみましょう。 いま (λ1, λ2) = (0, 0) と仮定します。 男は両方のタイプでOをプレイするのですね。 このときタイプ1(Loving)の女の最適反応はO、 タイプ2(Leaving)の最適反応はFになります。 逆に (μ1, μ2) = (0, 1) と仮定しましょう。 男が各タイプでOをプレイするのは最適反応でしょうか。 Pessimist（タイプ1）について考えてみましょう。 彼は女がLovingである確率をρLと考えます。
女の (O, F) を前提とすると、彼は F をプレイすることによって期待利得 0ρL + 3(1-ρL) = 3-3ρL を得ます。 O をプレイすることによって期待利得 1ρL + 0(1-ρL) = ρL を得ます。したがって ρL ≧ 3-3ρL 、すなわち ρL ≧ 3/4 ならば O は彼の最適反応になります。
Optimist（タイプ2）について考えてみましょう。 彼は女がLovingである確率をρHと考えます。
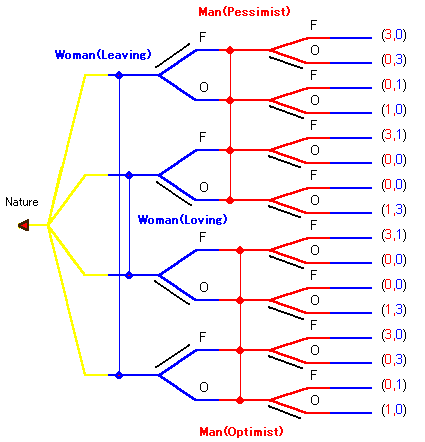
女の (O, F) を前提とすると、彼は F をプレイすることによって期待利得 0ρH + 3(1-ρH) = 3-3ρH を得ます。 O をプレイすることによって期待利得 1ρH + 0(1-ρH) = ρH を得ます。したがって ρH ≧ 3-3ρH 、すなわち ρH ≧ 3/4 ならば O は彼の最適反応になります。 いまρL≧3/4としましょう。 ρH＞ρL（定義）なのでρH＞3/4です。 このとき女の (O, F) に対するOは両方のタイプの男にとって最適反応となります。 逆に男の (O, O) に対しては女の (O, F) は最適反応です。 ρL≧3/4のとき (λ1, λ2, μ1, μ2) = (0, 0, 0, 1) はベイズ・ナッシュ均衡になります。
◆参考文献
|
