 男と女３ |
 |
|
前回の続きです。
前回求めたベイズ・ナッシュ均衡（純粋戦略）はqの値に関係ありませんでした。
（qはプレーヤーたちの考えるPessimistの存在率です。）
ρL≧1/4のとき： (λ1, λ2, μ1, μ2) = (1, 1, 1, 0) ρL≧3/4のとき： (λ1, λ2, μ1, μ2) = (0, 0, 0, 1) はベイズ・ナッシュ均衡 ということでqの値に関係ありませんでした。 これは男が両方のタイプで同じ戦略をとっているからです。 今回は男がそれぞれのタイプで異なる戦略をとる場合を考えます。
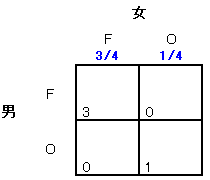
さてこのゲームでは男女のペアの事前確率分布は下の表で与えられます。 ここでρLはPessimistの考えるLovingの確率、 ρHはOptimistの考えるLovingの確率です。
いま q=1/2, ρL=1/4, ρH=3/4 としましょう。 するとこのとき (λ1, λ2, μ1, μ2) = (1, 0, 0, 1) はベイズ・ナッシュ均衡になります。 確認してみましょう。
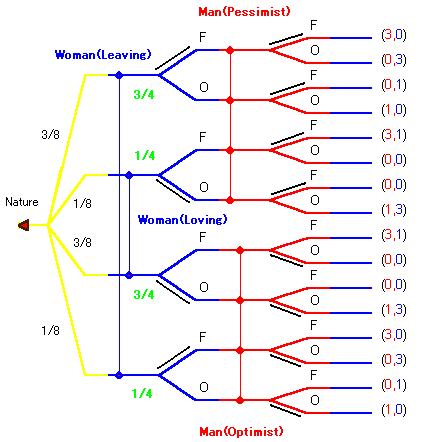
まず自然が男女のペア (男, 女) = (Pessimist, Loving), (Pessimist, Leaving), (Optimist, Loving), (Optimist, Leaving) をそれぞれ 1/8, 3/8, 3/8, 1/8 の確率で選びます。
プレーヤーたちはそれぞれのタイプで異なる信念をもちます。 男は いっぽうの女ですが、男のタイプに関する事前の予想はq=1/2です。 ところが女は自分のタイプを知っているので、 上の同時確率分布から自分のタイプを所与としたときの条件つき確率が計算できて
Lovingならば男がPessimistである確率を q1=(1/8)/{(1/8)+(3/8)}=1/4 と考えます。 つまり女は自分の個人情報を用いて男のタイプに関する予想を修正するのです。 自分のタイプがわかる前は q=1/2 という予想だけれど、自分のタイプがわかったからにはこれを上のように修正します。 男と女はこれらの条件つき確率を用いて戦略を考えます。
いま男はPessimistタイプではF、OptimistタイプではOをとっているとします。 このときの女の最適反応を考えましょう。 まずLovingタイプです。彼女はPessimistの確率を1/4、 Optimistの確率を3/4と考えます。 したがって 相手は確率1/4でFを、確率3/4でOをプレイしてくると考えます。 Fのときの期待値は(1/4)*1=1/4、Oのときの期待値は(3/4)*3=9/4です。 Oが最適反応になります。
つぎにLeavingタイプです。 彼女はPessimistの確率を3/4、 Optimistの確率を1/4と考えます。 したがって 相手は確率3/4でFを、確率1/4でOをプレイしてくると考えます。 Fのときの期待値は(1/4)*3=3/4、Oのときの期待値は(3/4)*1=3/4です。 FとOは無差別になります。とくにFは最適反応になります。
逆に女はLovingタイプではO、LeavingタイプではFをとっているとします。 このときの男の最適反応を考えましょう。 まずPessimistタイプです。彼はLovingの確率を1/4、Leavingの確率を3/4と考えます。 したがって相手は確率1/4でOを、確率3/4でFをプレイしてくると考えます。 Fのときの期待値は(3/4)*3=9/4、Oのときの期待値は(1/4)*1=1/4です。 Fが最適反応になります。
つぎにOptimistタイプです。彼はLovingの確率を3/4、Leavingの確率を1/4と考えます。 したがって相手は確率3/4でOを、確率1/4でFをプレイしてくると考えます。 Fのときの期待値は(1/4)*3=3/4、Oのときの期待値は(3/4)*1=3/4です。 FとOは無差別になります。とくにOは最適反応になります。
こうして (λ1, λ2, μ1, μ2) = (1, 0, 0, 1) はベイズ・ナッシュ均衡になることがわかります。
念のために (λ1, λ2, μ1, μ2) = (0, 1, 1, 0) はベイズ・ナッシュ均衡にはならないことを確認してみましょう。
いま男はPessimistタイプではO、OptimistタイプではFをとっているとします。 このときの女の最適反応を考えましょう。 まずLovingタイプです。彼女はPessimistの確率を1/4、 Optimistの確率を3/4と考えます。 したがって 相手は確率1/4でOを、確率3/4でFをプレイしてくると考えます。 Fのときの期待値は(3/4)*1=3/4、Oのときの期待値は(1/4)*3=3/4です。 FとOは無差別になります。とくにFは最適反応になります。
つぎにLeavingタイプです。 彼女はPessimistの確率を3/4、Optimistの確率1/4と考えます。 したがって 相手は確率3/4でOを、確率1/4でFをプレイしてくると考えます。 Fのときの期待値は(3/4)*3=9/4、Oのときの期待値は(1/4)*1=1/4です。 Fが最適反応になります。（Oは最適反応になりません。）
こうして (λ1, λ2, μ1, μ2) = (0, 1, 1, 0) はベイズ・ナッシュ均衡にはならないことがわかります。
◆参考文献
|
