 ベイズ完全均衡 |
 |
|
つぎのようなゲームを考えてみてください。
 この交互進行ゲームでは、部分ゲームは全体のゲームだけなので、 部分ゲーム完全均衡はナッシュ均衡と同値になります。 このツリーをテーブルに直すとつぎのようになり、ナッシュ均衡は２つあることがわかります。
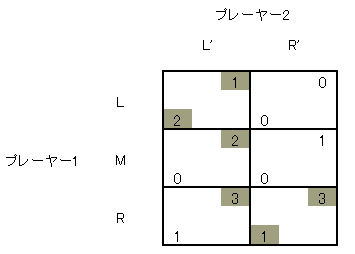
 したがって部分ゲーム完全均衡は (L, L') , (R, R') の２つということになります。 ところがいま、このうちの (R, R') を取り上げてみましょう。 この結果はつぎのようにして生じるかもしれません。 つまり、もし2の手番になったとき、2は R' を選ぶことで1の利得をゼロにすることができます。そこで2は1に「 R を選べ。さもなくば R' を選ぶぞ」と脅しをかけるのです。そして1がその脅しに屈するのです。 しかしこれはちょっと考えにくいです。というのは、明らかに この脅しには信憑性がないからです。つまり2は自分の手番になったとき、 L' を選ぶのが絶対優位です。このように (R, R') というのはどうもゲームの解としてよくないと思われます。
これから紹介するベイズ完全均衡というのは、このようなあやしい均衡を排除するものです。 いま、つぎのような仮定をおいてみてはどうでしょう。
すなわち、プレーヤー2は、もし自分の手番がきたなら、自分がどっちの点にいるかということについて何らかの見積もりをしなくてはならないとするのです。この信念（確率分布）を (p, 1-p) としましょう。
 そしてプレーヤー2はこの信念 (p, 1-p) を所与としたとき最適に行動するとします。
L' をプレイしたときの期待利得： 1*p + 2*(1-p) = 2-p となり、いかなる p についても 2-p > 1-p となるので、プレーヤー2の最適行動は L' となります。いいかえれば、信念を所与とするとき、2の R' という戦略は合理的でなくなります。 こうして、「プレーヤーは信念をもち、その信念のもとで最適に行動する」と仮定するだけで、もっともらしくない均衡 (R, R') を排除することができます。 さて、以上はベイズ完全均衡の最初のステップです。 じっさい、ベイズ完全均衡というのはこの条件に
という条件をプラスしたものをいいます。
信念が理にかなっている？どういうことでしょう。 いま部分ゲーム完全均衡 (L, L') を考えます。 するとプレーヤー1の均衡戦略 L を前提としたとき、プレーヤー2は自分がどっちの点にいるかわかります。つまり p = 1 と計算できます。 「信念が理にかなっている」というのはいいかえれば「信念は均衡戦略とベイズルールから決定される」ということになります。 したがってこのゲームでベイズ完全均衡というのは (L, L') , p = 1 ということになります。 ナッシュ均衡と信念の組み合せのうち、アンダーラインを引いた２つの条件をみたすものです。これがこのゲームの解としてふさわしいです。
◆参考文献
|
