 チャーミーの挑戦３ |
 |
「チャーミーの挑戦２」の設定を少しだけ変えてみましょう。チャーミーはセクシーの行動をみたあとに行動できるとしてみるのです。
 VS  チャーミーいま、新しいゲームはつぎのツリーで表現できるとします。
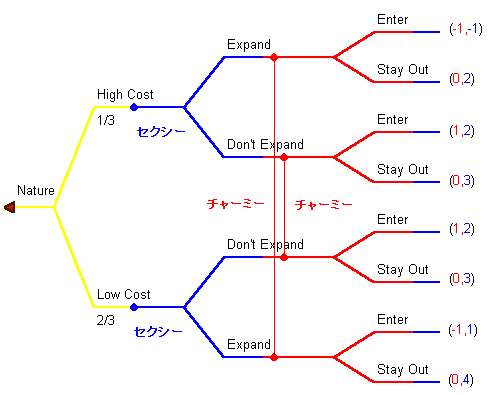
まず自然が 1/3 の確率で High Cost 、 2/3 の確率で Low Cost を選びます。 自然の行動をみたあとでセクシーは Expand か Don't Expand を選びます。 セクシーの行動をみたあとでチャーミーは Enter か Stay Out を決めます。 ここでチャーミーはセクシーのタイプがわからないので、線で結んでいます。 たとえば、セクシーが Expand を選ぶのを観察したとしても、それが High Cost のセクシーなのか Low Cost のセクシーなのかわからないのです。 さてこのゲームでは、＜セクシーは High Cost なら Don't Expand 、 Low Cost なら Expand という戦略をとり、いっぽうのチャーミーはもし Expand を観察したなら Stay Out 、もし Don't Expand を観察したなら Enter をとる＞という戦略の組はベイズ完全均衡になることがわかります。 いま、セクシーは High Cost なら Don't Expand 、 Low Cost なら Expand という戦略をとっているとします。するとチャーミーの合理的な信念というのは、情報集合 A では (High: 0, Low: 1) であり、 情報集合 B では (High: 1, Low: 0) です。 この信念のもとでのチャーミーの最適な行動を考えましょう。 するとチャーミーの情報集合 A での Stay Out は最適になっています。（期待利得 -1*0+(-1)*1=-1 と 0 を比較する。）いっぽう情報集合 B での Enter は最適になっています。（期待利得 1*1+1*0=1 と 0 を比較する。）よってこの信念のもとではチャーミーの (Stay Out - Enter) は最適になっています。
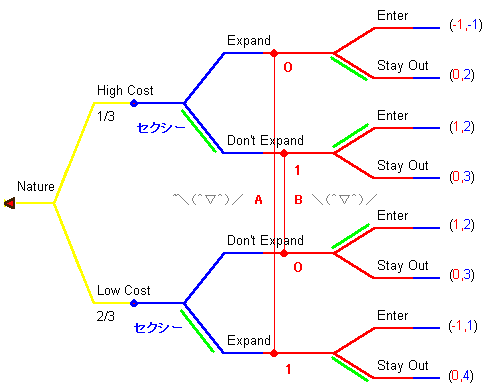
では逆にチャーミーが (Stay Out - Enter) という戦略をとっているとしましょう。 するとセクシーが High タイプならDon't Expand 、 Low タイプなら Expand をとるのは最適反応になっています。 こうして戦略の組 (セクシー, チャーミー) = (Don't Expand - Expand , Stay Out - Enter) および信念 {Expand: ( High: 0, Low: 1), Don't Expand: ( High: 1, Low: 0)} はベイズ完全均衡を構成することがわかります。
「サプライズ・ギフト」で見た「セパレーティング均衡」「プーリング均衡」もじつは ベイズ完全均衡です。
case1: c > 2 の場合 セパレーティング均衡
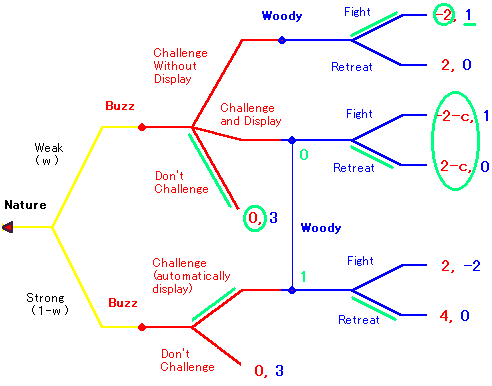
いまバズの (Don't Challenge - Challenge) を前提とすると、ウッディの合理的な信念は (0, 1) です。そこで Retreat は最適になっています。（期待利得 1*0+(-2)*1=-2 と 0 を比較する。）逆にウッディの Retreat を前提とするとバズの (Don't Challenge - Challenge) は最適になっています。 case2: c < 2 の場合 プーリング均衡
いまバズの (Challenge - Challenge) を前提とすると、ウッディの合理的な信念は (w, 1-w) です。そこで w < 2/3 とすると Retreat は最適になります。（期待利得 1w-2(1-w)= 3w-2 < 0 と 0 を比較する。）逆にウッディの Retreat を前提とするとバズの (Challenge - Challenge) は最適になっています。
◆参考文献
|
