 サプライズ・ギフト |
 |
|
"TO INFINITY AND BEYOND!" いま、ウッディ社は新しい戦いに直面しています。
ウッディ社が独占支配するあるマーケットに、バズ・ライトイヤーという、
これまでになかったタイプの敵が現れたのです。
ウッディは、この新しい敵が革新的な技術をもつならば、勝負をあきらめ、市場から撤退しようと考えています。 じっさい戦争が開始された場合、ウッディは弱いタイプのバズならば蹴散らすことができるのですが、強いタイプのバズには勝てそうもないのです。 プレーヤーの利得はつぎのようになります。
さて、いまバズは、自分が強いことを証明するために、何かをウッディに見せつけることができるとしましょう。たとえば、優れた技術をもつと思わせるような「試作品」をディスプレイ（展示）することができるとします。もしバズが本当に強いならば、コストゼロでディスプレイすることができます。 ところがバズは、本当は弱いのに、無理にディスプレイして強いふりをしようとすることもできます。ただこのときはコスト c がかかります。 ゲームは下のツリーで表現できます。
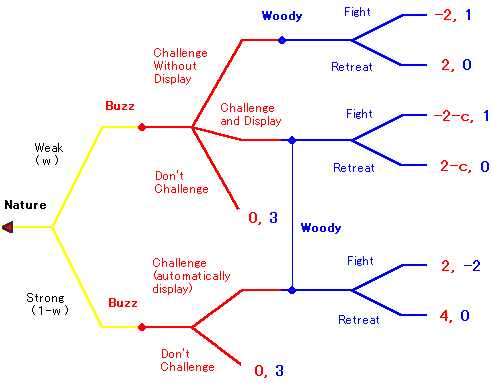
まず自然が確率分布 (w, 1-w) でバズのタイプを選びます。バズは自然の選択を見た後に行動します。 弱いタイプの場合は３つの選択肢があります。すなわち「ディスプレイなしにチャレンジ」 「チャレンジ時にはディスプレイする」「チャレンジしない」。 強いタイプの場合は２つの選択肢があります。すなわち「チャレンジする（自動的にディスプレイ）」「チャレンジしない」。 そしてバズの行動を見た後、ウッディが動きます。 もしバズがディスプレイつきでチャレンジしてきた場合は、ウッディは相手のタイプがわからないので、線で結んでいます。 なお、バズがチャレンジしない場合は現状維持で、利得は (バズ, ウッディ) = (0, 3) となります。 さて、このゲームはどういう結果になるでしょう。
case1: c > 2 の場合 いま、 c > 2 とします。 ディスプレイするコストが高いケースですね。 この場合、まずツリーをみてわかることは、 バズがディスプレイなしでチャレンジしてきたときはバズは弱いタイプであるということで、そしてこのときウッディは戦うということです。（利得 1 と 0 を比較する。）
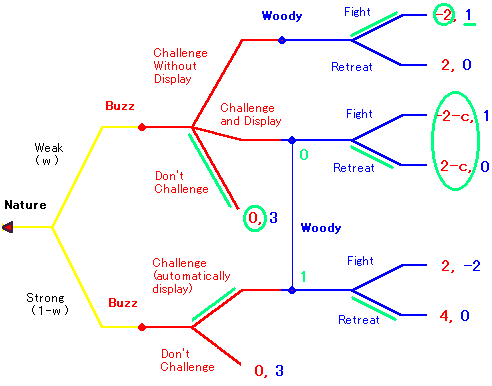
そこでバズの戦略を考えましょう。まずバズは、弱いタイプであるならば、チャレンジしないのが最適であることがわかります。なぜなら、ディスプレイなしでチャレンジした場合は利得 -2 、ディスプレイつきでチャレンジした場合はウッディがどう出ようと利得はマイナス、チャレンジしなければ利得は 0 だからです。つぎに、バズが強いタイプであるならば、チャレンジするのが最適であることがわかります。チャレンジした場合はウッディがどう出ようと利得はプラス、チャレンジしなければ利得は 0 だからです。 ＜バズの戦略： 弱いタイプならばチャレンジしない。強いタイプならばチャレンジする。＞
こんどはウッディの戦略を考えましょう。 まず、バズがディスプレイなしでチャレンジしてきたときは、戦ったほうがよい ことがわかります。つぎに、下の情報集合について考えます。 これはバズがディスプレイつきのチャレンジをしてきた場合、どっちのタイプかわからないので線で結んでいたのでした。ところがいまや、バズがディスプレイつきでチャレンジしてくるのは、それが強いタイプであるときだということがわかっています。 （これはいいかえれば、もしディスプレイつきのチャレンジを観察した場合、下の点にいる確率を 1 と計算できるということです。）したがってウッディは退却するのが最適になります。（期待利得 1*0+(-2)*1 = -2 と 0 を比較する。） ＜ウッディの戦略： ディスプレイなしのチャレンジを観察した場合、戦う。ディスプレイつきのチャレンジを観察した場合、退却する。＞ こうして、試作品を作るコストが高い場合は、弱いタイプのバズが強いタイプのふりをしてチャレンジしてこない、すなわち「紛れ」は生じないことがわかります。 これはセパレーティング均衡（分離均衡）とよばれます。ディスプレイの有る無しで２つのタイプをセパレートできる（分けることができる）からです。
case2: c < 2 の場合 いま、 c < 2 とします。 ディスプレイするコストが低いケースですね。 この場合、ハッタリのコストが低いということなので、 弱いタイプもチャレンジしてくるかもしれません。 じっさい、ウッディがディスプレイつきのチャレンジを観察した場合に退却すると仮定すると、弱いタイプでもチャレンジしたほうがよいです。（ 2-c > 0 なので。）
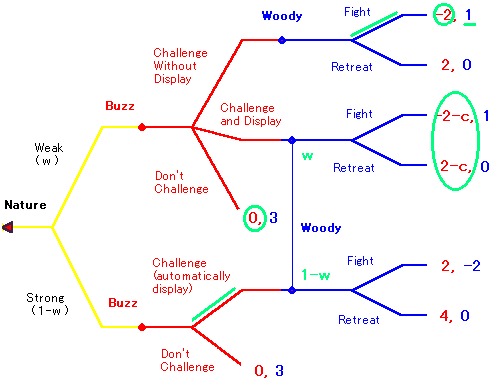
いっぽうのウッディの戦略を考えてみましょう。 まず、弱いタイプのバズもディスプレイつきのチャレンジをしてくると仮定します。 するとこの場合、ディスプレイを観察しても何も推論することができません。そこでウッディは、弱いタイプのバズと直面している確率を w 、強いタイプのバズと直面している確率を 1-w と見積もるしかないです。そして、線で結ばれたところでは期待利得を計算して行動を決めることになります。
戦った場合の期待利得： 1w + (-2)(1-w) = 3w - 2
となります。 3w - 2 > 0 、すなわち w > 2/3 なら戦ったほうがよく、 3w - 2 < 0 、すなわち w < 2/3 なら退却したほうがよいことになります。 いま、事前確率について w < 2/3 であるとしましょう。 もともと強いタイプが多い（ > 1/3 ）と考えられる場合ですね。 そこで再びバズとウッディの戦略を考えます。 いまウッディは、＜ディスプレイつきのチャレンジを観察した場合は退却する＞という戦略をとっているとしましょう。するとこれに対するバズの最適反応は＜弱いタイプでもディスプレイつきのチャレンジをする＞です。逆に、バズが＜弱いタイプでもディスプレイつきのチャレンジをする＞という戦略をとっているとき、これに対するウッディの最適反応は＜ディスプレイつきのチャレンジを観察した場合は退却する＞です。 したがってお互いにこの戦略をとっているとき、バズもウッディも戦略を変える誘因がありません。
こうして、試作品を作るコストが低く、なおかつもともと強いタイプが多い（ > 1/3 ）と考えられる場合は、弱いタイプのバズが強いタイプのふりをしてチャレンジしてくる、 というのが均衡になることがわかります。 つまり「紛れ」が生じてしまう均衡です。 この均衡では、どちらのタイプのバズもディスプレイを使ってチャレンジしてきます。 ディスプレイの有る無しで２つのタイプがセパレートできないので、ゲームの均衡はプーリング均衡（一括均衡）とよばれます。（ pool は 「いっしょにする」という意味です。）
◆参考文献
|
