 サプライズ・ギフト2 サプライズ・ギフト2 |
 |
|
前回の「サプライズ・ギフト」では「c>2の場合」と「c<2かつw<2/3の場合」 の2つのケースを考えました。今回は最後の可能性である「c<2かつw>2/3の場合」を考えます。ディスプレイのコストが低くなおかつ弱いタイプのバズが多いと見積もられる場合ですね。 バズの戦略から考えましょう。まず弱いタイプの場合です。 ディスプレイなしでチャレンジするのは考慮からはずせます。 問題はディスプレイつきでチャレンジするか、チャレンジしないかということです。 ウッディがファイトしてくるならチャレンジしないほうがよく、退却するならチャレンジしたほうがよいです。つぎに強いタイプの場合です。このときはチャレンジしたほうがよいです。
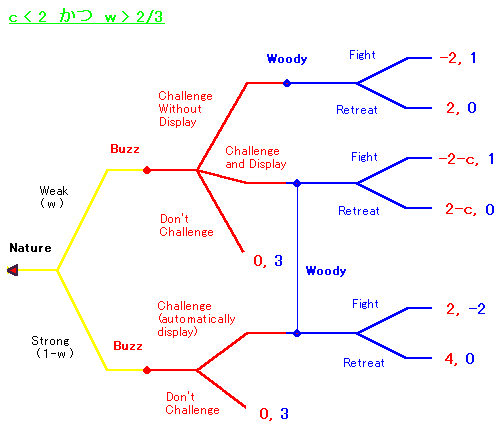
ウッディの戦略を考えましょう。 バズがディスプレイなしでチャレンジしてくるというのは考慮からはずせます。 問題はバズのタイプを見分けられないということです。 いま事前確率は w>2/3 です。 まず弱いタイプのバズもディスプレイつきのチャレンジをしてくると仮定しましょう。ウッディは、弱いタイプのバズと直面している確率を w 、強いタイプのバズと直面している確率を 1-w と見積もるしかないです。戦った場合の期待利得は 1w+(-2)(1-w)=3w-2 になります。w>2/3 なので戦ったほうがよいです。 ところが逆にウッディが戦うと仮定すると弱いタイプのバズはチャレンジしないほうがよいことになります。戦略の整合性がとれないことになります。

では弱いタイプのバズはチャレンジしてこないと仮定しましょう。 ウッディは下の点にいる確率を1と考えます。ウッディは退却したほうがよいです。ところが逆にウッディの退却を前提とすると、弱いタイプのバズもチャレンジしたほうがよいことになります。やはり整合的になりません。 何かいやな予感がします。こういうふうに戦略がかみ合わないときは混合戦略を考えるしかないのでした。
弱いタイプのバズがチャレンジする確率をp、 ウッディがディスプレイつきのチャレンジをみたときにファイトする確率をqとします。
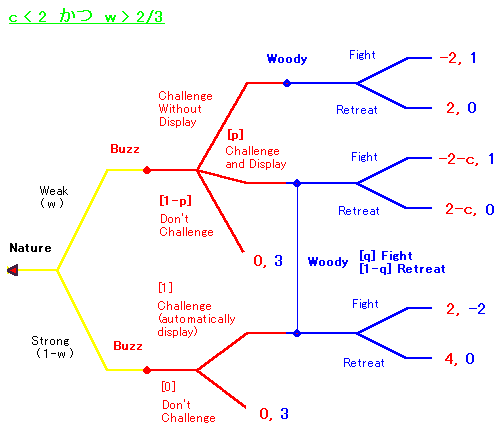
バズとウッディの混合戦略がかみ合うような p, q を求めましょう。 ウッディの戦略から考えます。 ポイントはディスプレイつきのチャレンジを観察したとき、 それがどっちのバズのものかということです。 サンプルがチョコだったときそれがどっちの箱のものかということです。 ディスプレイつきのチャレンジを観察したという条件のもとで バズが弱いタイプである確率を求めます。 ベイズルールによりこれは wp/(wp+1-w) です。 ディスプレイつきのチャレンジを観察したという条件のもとで バズが強いタイプである確率を求めます。 ベイズルールによりこれは (1-w)/(wp+1-w) です。 (余事象を計算してもよいです。) あとはいつもと同じです。 ウッディが上の点にいる確率は wp/(wp+1-w) 、下の点にいる確率は (1-w)/(wp+1-w) です。Fightの期待値は
1(wp/(wp+1-w)) - 2(1-w)/(wp+1-w)
になります。 いまバズが上式=0とするようなpを使うとしましょう。すなわちpは
wp-2+2w=0
ということです。 このときウッディはFightとRetreatのどっちを選んでも同じになります。 FightとRetreatは無差別になります。 期待値が同じものをどうこうミックスしたところで何も変わらないので すべてのqは最適反応になります。

バズの戦略を考えましょう。 弱いタイプのときにチャレンジする場合、 期待利得は
q(-2-c)+(1-q)(2-c)
になります。 いまウッディが上式=0にするようなqを使うとしましょう。 すなわち
2-c-4q=0
ということです。 このとき弱いタイプのバズはチャレンジしてもしなくても同じになります。 Challenge と Don't Challenge は無差別になります。 期待値が同じものをどうこうミックスしたところで何も変わらないので すべてのpは最適反応になります。

いま p=2(1-w)/w, q=(2-c)/4 という戦略の組を考えましょう。 p=2(1-w)/w に対してはすべてのqが最適反応なのでとくに q=(2-c)/4 は最適反応になります。逆に q=(2-c)/4 に対してはすべてのpが最適反応なのでとくに p=2(1-w)/w は最適反応になります。 p=2(1-w)/w, q=(2-c)/4 は互いに最適反応になります。
(p, q)=(2(1-w)/w, (2-c)/4) 、これがゲームの均衡です。 たとえば w=0.8, c=1 とすると 均衡は p=2*0.2/0.8=0.5, q=0.25 となります。 wを0.8にしたままcを0にかぎりなく近づけると 均衡は p=0.5, q=0.5 となり、 ウッディもバズもコインを投げて決めるのが正解ということになります。 こうしてc<2かつw>2/3の場合は ゲームは不確実性の残る状態となることがわかります。 ゲームの均衡(ベイズ完全均衡)はセミセパレーティング均衡とよばれます。
かなり複雑でしたので、じっさいに具体的な数字を入れて確認してみましょう。 いま w=0.8, c=1 、ウッディとバズは混合戦略 p=0.5, q=0.25 をとっているとします。 ウッディの信念は 0.8*0.5/(0.8*0.5+0.2*1)=0.4/0.6=2/3 より (2/3, 1/3) となります。
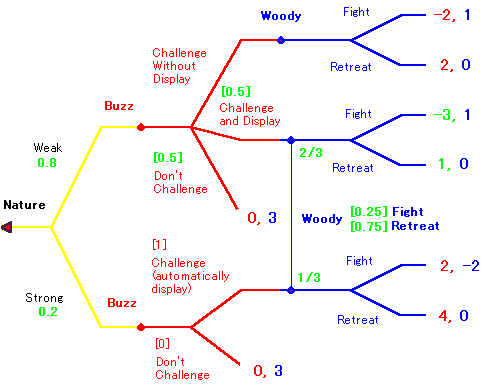
いまバズが p=0.5 をとっているとします。 このときウッディの Fightの期待値は 1(2/3)-2(1/3)=0 となります。 FightとRetreatは無差別になります。 期待値が同じものをどうこうミックスしたところで何も変わらないので、 すべてのqは最適反応になります。とくに q=0.25 は最適反応になります。 逆にウッディが q=0.25 をとっているとします。 弱いタイプのバズがチャレンジするときの期待利得は -3*0.25+1*0.75=0 となります。 Challenge と Don't Challenge は無差別になります。 期待値が同じものをどうこうミックスしたところで何も変わらないので、 すべてのpは最適反応になります。とくに p=0.5 は最適反応になります。 すべてが整合的になっています。すなわちベイズ完全均衡です。
◆参考文献
ANDY'S ROOM

|

