モラルハザード
|
火災保険について考えましょう。
加入者は火事を起こしても補償されるので、
火の始末にあまり気を使わなくなりますし、
極端な場合、自ら放火するインセンティブがあります。
加入者は、自分の行動が保険会社には完全にはわからないのをいいことに、
保険会社にとって望ましくない行動をとります。
契約関係にあるAとBについて、Aの行動がBには完全には観察あるいは強制できないために、AがBにとって望ましくない行動をとる。 このようなことは経済学ではモラルハザードと呼ばれます。（もともとモラルハザードは保険業界の用語でした。） モラルハザードはゲーム理論では下のようなモデルで記述できます。
経営者と従業員の契約を考えましょう。（会社には1人の経営者と1人の従業員しかいません。）経営者は賃金体系（インセンティブ・スキーム）についていくつかの戦略をもっています。 一方の従業員は頑張るか怠けるかの2つの戦略があります。 従業員が頑張ると、会社は0.6の確率で「良い」業績、0.3の確率で「普通の」業績、0.1の確率で「悪い」業績をあげます。従業員が怠けると、会社は0.1の確率で「良い」業績、0.3の確率で「普通の」業績、0.6の確率で「悪い」業績をあげます。 （ここで従業員の努力の程度と会社の業績はストレートに結びつくわけではないことに注意してください。確率的に決まるのです。） ゲームツリーでは下のように描けます。 |
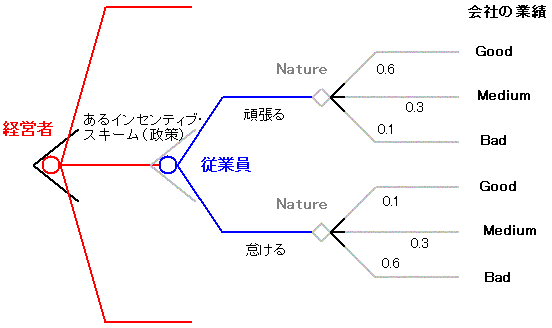
| ここで会社の「良い」業績、「普通の」業績、「悪い」業績の水準を それぞれ g, m, b で表すとします。また従業員の賃金は会社の業績水準によって決まり、 それぞれは Wg, Wm, Wb で表されるとします。すると従業員の努力のコストを、頑張る場合は C 、怠ける場合は c としたとき、経営者と従業員の利得は下のようになります。 |
|
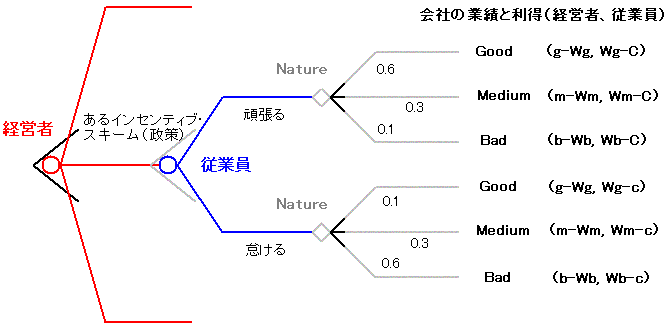
ツリー中の「あるインセンティブ・スキーム（政策）」について考えましょう。 もし経営者が「固定賃金政策」をとったとします。 つまり Wg = Wm = Wb (= w) とする戦略です。（下図。） |
|
このとき従業員の最適反応はどうなるでしょうか。
従業員の期待利得は
頑張った場合： 0.6(w-C)+0.3(w-C)+0.1(w-C) = w-C
となります。 C＞c なので w-C ＜ w-c です。 したがって怠けるのが最適反応になります。
◆参考文献
|
