Game Theory 101

定理
1変数の関数をコンパクト凸な定義域で考える。もし値域が定義域と同じ集合に含まれ、かつ関数が連続ならば、関数は必ず不動点をもつ。

この定理で述べたのは、1つの実数に1つの実数が対応するような簡単な関数についてです。これを1つの点に1つの点が対応するような関数に拡張したのがブラウワーの不動点定理です。

いま左の円の中の各点について、座標をそれぞれ1/2倍したものが対応するような関数を考えます。たとえば (1, 0) には (0.5, 0) が、(0.5, 0.5) には (0.25, 0.25) が対応するのですね。

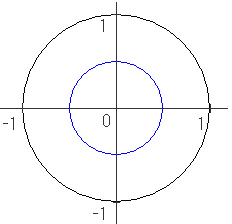
対応したもの（アウトプットされたもの）の集合は右の小さい円（の内部）で表わされます。そしてこの関数には明らかに不動点になるものがあります。 (0, 0) ですね。

不動点定理（Brouwer）
点を点に対応させる関数をコンパクト凸な定義域で考える。もし値域が定義域と同じ集合に含まれ、かつ関数が連続ならば、関数は必ず不動点をもつ。

上の例の場合、定義域の集合は左の円の内部（境界含む）です。この集合は平面版の [0, 1] といってよいです。すなわち広さに限りがあり（有界）、境界が集合に含まれ（閉）、どの2点をとってもその結ぶ線分は集合に含まれています（凸）。じっさいこの集合（定義域）はコンパクト凸といいます。

また値域の集合が定義域の集合に含まれるのは明らかでしょう。関数が連続ということはつぎのように考えます。

いま左の円のある1点と、これをほんの少しだけ動かした点を考えます。たとえば (0.5, 0.5) と (0.5, 0.52) ですね。関数によって2点に対応する点はそれぞれ (0.25, 0.25) と (0.25, 0.26) です。これらの2点もやはり互いにすぐ近くにあります。このようなことは左の円のどんな近い2点についても言えます。こういう場合、関数は連続であるといいます。

一般的に、点のわずかな変化に対して対応する点もわずかにしか変化しないとき、関数は連続といいます。（1変数の場合もこれはあてはまります）

なおブラウワーの不動点定理の証明ですが、あまりに大変なのでここではやりません。定理のイメージだけを具体例からつかんでおいてください。