凸、有界、閉、コンパクト
|
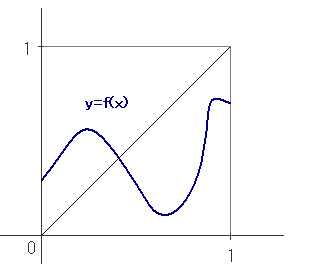
この [0, 1] は必ずしも [0, 1] じゃなくてよいです。 たとえば [0, 2] にかえても定理は成り立ちます。 これは目盛りをかえればいいだけなので自明でしょう。
しかし [0, 1] を [0, 1) にかえると成り立たなくなります。 [0, 1) とは0以上1未満の実数の集合です。 （ここで [0, 1] のような集合を閉区間というのに対し、 [0, 1) のような集合を（半）開区間といいます。） これはたとえば y=0.5x+0.5 で考えるとわかります。
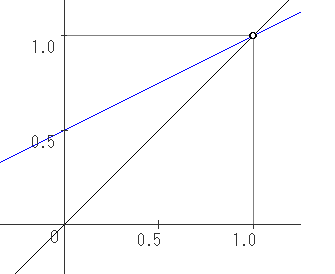
[0, 1] なら x=1 で不動点をもつのですが、 x=1 が定義域に含まれないので不動点をもたないのです。 同様なことが (0, 1] や (0, 1) でも言えます。 また定義域が分断していたり、無限区間だったりしてもいけません。 これは下のような図をイメージすればわかります。
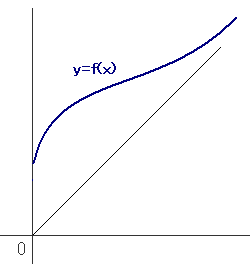
定義域が分断してないということは、数学では凸（とつ）という言葉で言い表されます。つまり定義域のどの2点をとってきても、それらを結ぶ線分が定義域に含まれる とき、定義域は凸であるといいます。たとえば [0, 1] は凸ですが、上の図（左）のように分断している場合は凸ではありません。また区間に限りがあるということは、数学では有界と表現されます。上の図（右）の定義域は有界ではありません。 以上をまとめると [a, b] のような区間（集合）は、閉で凸で有界であるといいます。また有界かつ閉のものをコンパクトといいます。 そこで一般的には
というふうに書けるのです。
◆参考文献
|
