不動点定理入門
|
前回説明したように不動点とは
x* ∈ F(x*) となる x* のことを言います。 元の点 x* に対してFが返した集合を F(x*) とするとき、 F(x*) の中に x* が含まれていれば、 x* は不動点なのです。
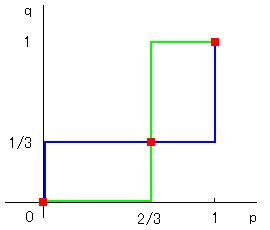
アイとノノのゲーム（関数）でいえば
x* = (0, 0) ∈ (0, 0) の3つが不動点です。 さて問題はどんなゲームにも、つまりどんな一般の関数にも不動点があるのかどうかということです。 これを考えるためには、まず最も簡単な（アイとノノのゲームよりも簡単な） 関数を調べてみることから始めます。
中学のころからおなじみの関数といえば、 y=0.5x+0.2 のような、1つの数値に1つの数値が決まるものでしょう。 いま f(x) = 0.5x+0.2 を定義域 [0, 1] で考えます。 x を0から1の範囲で動かすのですね。
このとき関数は不動点をもつでしょうか？ もちます。 x=0.4 は不動点です。なぜなら f(0.4)= 0.2+0.2 = 0.4 となるからです。 どうやってこれを見つけたかというと 方程式 0.5x+0.2 = x を解きました。 一般に f(x) = x を解けば不動点が求められます。 ところがこれは y=0.5x+0.2 と y=x の交点を求めるのと同じです。 そこで下のように図をかいて不動点の見当をつけることができます。
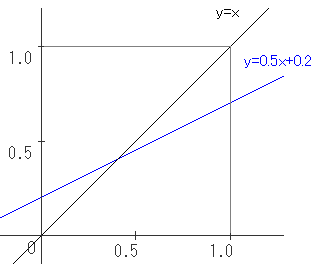
（ここで関数の値域が [0.2, 0.7] で、 [0, 1] に含まれることに注意しておいてください。）
上の例から一般に 1変数の関数を定義域 [0, 1] で考えた場合、 値域もまた [0, 1] に含まれるならば、 その不動点は y=f(x) と y=x の交点になる ということが わかるとおもいます（下図参照）。
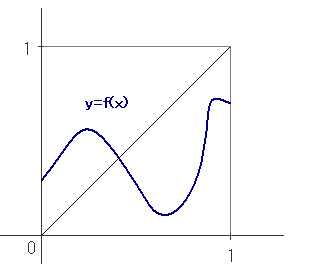
そこで不動点の存在は、関数のグラフが「45度線」と交わるかどうかという、 割と簡単な問題に帰着されます。 上の45度線を「川」とみなし、 いま正方形の左の辺から右の辺に行くとしましょう。 （出発点と到着点は辺のどの点でもいいです。） このとき必ず川を横切らないとだめなことが確かめられるとおもいます。 このことによって、グラフが定義域で「つながっている」ならば、 関数は必ず不動点をもつということが言えるのがわかります。
◆参考文献
|
