Game Theory 101

不動点定理（Brouwer）
点を点に対応させる関数をコンパクト凸な定義域で考える。もし値域が定義域と同じ集合に含まれ、かつ関数が連続ならば、関数は必ず不動点をもつ。

ブラウワーの不動点定理は、1つの点に1つの点が対応するような関数について述べたものです。これを1つの点に1つの集合が対応するような関数に拡張したものが角谷の不動点定理です。

これは点に集合が対応するような関数で最も簡単なものです。（1次元→1次元の対応。点に対し点が返ってくるときも、それは1つの要素しかもたない集合と考えます。）たとえば x=0 には y=0 が対応し、 x=0.5 には y=[0, 1] が対応します。

この関数には不動点が3つ存在します。 x=0, x=0.5, x=1 ですね。

不動点定理（Kakutani）
点を集合に対応させる関数をコンパクト凸な定義域で考える。もし値域が定義域と同じ集合に含まれ、かつ関数が連続ならば、関数は必ず不動点をもつ。

上の例の場合、定義域の集合は [0, 1] でコンパクト凸です。また返ってくる集合はどんなものも [0, 1] に含まれるので、値域は定義域と同じ集合に含まれることになります。（ややこしい言い方ですが、グラフをみれば値域は明らかに 0≦y≦1 です。）

また関数のグラフは（これまでのとちょっと意味が違いますが）つながっているので連続といえます。

われわれはある戦略の組 (p, q) をインプットすると、やはり戦略の組としてある (p, q) を返す関数Fについて考えていたのでした。

たとえばFは (p, q) = (1/3, 2/3) に対しては (p, q) = (1, 0) を返し、 (p, q) = (2/3, 2/3) に対しては (p, q) = (1, [0, 1]) を返します。つまり点に集合を対応させています。

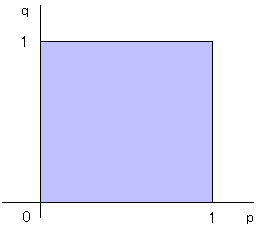
この集合は広さに限りがあり（有界）、境界が集合に含まれ（閉）、どの2点をとってもその結ぶ線分は集合に含まれています（凸）。この集合（定義域）はコンパクト凸です。

返ってくる集合はどんなものも正方形に含まれるので、値域は定義域と同じ集合に含まれることになります。

連続性はどうでしょうか。これはちょっと考えるのが難しいです。そこで適当なアナロジーを使って考えます。（正しく取り扱うにはさらなる位相数学の知識が必要なのでここではあきらめます。）

いま関数Fはたとえば (2/3, 2/3) に対しては (1, [0, 1]) を返しますが、わずかに変化させた点 (0.67, 2/3) に対しては (1, 1) を返します。

これは先にあげた例の、 x=0.5 に対しては y=[0, 1] を返すが、わずかに変化させた点 x=0.51 に対しては y=1 を返す、というのに似てないでしょうか。

つまりノノの最適反応が p=2/3 を境に 0→[0, 1]→1 と変化していくように、 yは x=0.5 を境に 0→[0, 1]→1 と変化していきます。

こうして関数Fの「想像上の」グラフは、上のグラフのように「つながっている」と考えられます。

そういうわけで関数Fは連続ということが言えて、角谷の不動点定理の条件をすべて満たすことになります。

x^* = (0, 0) ∈ (0, 0)
x^* = (2/3, 1/3) ∈ ([0, 1], [0, 1])
x^* = (1, 1) ∈ (1, 1)