課税のトリック
|
キャンディーのマーケットを 考えます。 いまキャンディーの需要は q=-200p+1000 で表されるとします。 ここで p はキャンディーの価格（price）、 q は需要量（quantity demanded）です。 たとえば価格が p=4（ドル） なら→ q=200（単位） というふうに 需要量が決まります。 いっぽうキャンディーの供給は q=800p で表されるとします。 ここで p はキャンディーの価格（price）、 q は供給量（quantity supplied）です。 たとえば価格が p=4（ドル） なら→ q=3200（単位） というふうに 供給量が決まります。 均衡における価格と数量はそれぞれいくらになるでしょう。 均衡価格は需要量と供給量が一致することから
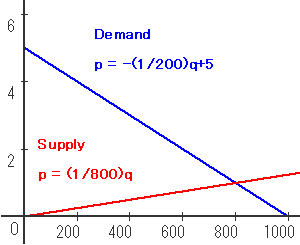
-200p+1000 = 800p です。 取引数量は q = 800（単位）です。 グラフにかくと下のようになります。 価格 p を縦軸、数量 q を横軸にとっていることに注意してください。 
さていま政府がキャンディーの取引に課税することにしたとしましょう。政府は
1. 消費者からお金を取り上げる： キャンディー1単位につき50セント の2つの方法があります。 そこで質問です。 いまあなたは消費者であるとします。 このとき方法1と2どちらがいいですか？ 反対にいまあなたは生産者であるとします。 このとき方法1と2どちらがいいですか？ 「消費者なら2、生産者なら1に決まってる」。 多くの方がそう思われるでしょう。 でもそれは間違っているのです。
方法1について考えましょう。 方法1は消費者の需要に影響を与えます。 たとえばある消費者はいままで3ドルのとき4単位を買っていたとしましょう。 するとこの消費者は2.5ドルのときはじめて4単位を買うようになります。 50セント余計に払うことを考慮に入れると、いままでより50セント安くてはじめてつじつまが合うからです。 同じ消費者はいままで4ドルのとき2単位を買っていたとしましょう。 するとこの消費者は3.5ドルのときはじめて2単位を買うようになります。 50セント余計に払うことを考慮に入れると、いままでより50セント安くてはじめてつじつまが合うからです。 このように消費者は以前より50セント下がったところで前と同じ量を 消費します。 すべての消費者について同様のことが言えます。 したがって いままで3ドルで400単位だった需要量が2.5ドルで400単位になり、 4ドルで200単位だった需要量が3.5ドルで200単位になります。 そこで 新しい需要曲線は下のようになります。 これは単にもとの曲線 p = -(1/200)q+5 を 垂直に0.5だけ下ろしたものです。 （これはいまはすこし理解しにくいとおもいますが、あとですぐに理解できるようになります。） 
均衡における価格を求めます。
p = -(1/200)q+4.5
q = 800p の連立方程式を解きます。
800p = -200p+900
均衡価格は90セントです。消費者はキャンディー1単位につき90+50=1ドル40セントを払うことになります。生産者はキャンディー1単位につき90セントを得ます。 これは50セントの負担を消費者40生産者10で分けたことになります。 （元の均衡価格は1ドルでした。）
方法2について考えましょう。 方法2は生産者の供給に影響を与えます。 たとえばある生産者はいままで3ドルのとき24単位を供給していたとしましょう。 するとこの生産者は3.5ドルのときはじめて24単位を供給するようになります。 50セントもっていかれることを考慮に入れると、いままでより 50セント高くてはじめてつじつまが合うからです。 同じ生産者はいままで4ドルのとき32単位を供給していたとしましょう。 するとこの生産者は4.5ドルのときはじめて32単位を供給するようになります。 50セントもっていかれることを考慮に入れると、いままでより 50セント高くてはじめてつじつまが合うからです。 このように生産者は以前より50セント上がったところで前と同じ量を 供給します。 すべての生産者について同様のことが言えます。 したがって いままで3ドルで2400単位だった供給量が3.5ドルで2400単位になり、 4ドルで3200単位だった供給量が4.5ドルで3200単位になります。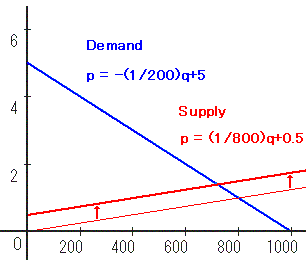 そこで 新しい供給曲線は下のようになります。 これは単にもとの曲線 p = (1/800)q を 垂直に0.5だけ上げたものです。 
均衡における価格を求めます。
p = (1/800)q+0.5
と q = -200p+1000 の連立方程式を解きます。
800p-400 = -200p+1000
均衡価格は1ドル40セントです。 消費者はキャンディー1単位につき1ドル40セントを払います。 生産者はその1ドル40セントのうち50セントを政府に払うことになり、 1単位につき差し引き90セントを得ます。 これは50セントの負担を消費者40生産者10で分けたことになります。 （元の均衡価格は1ドルでした。）
こうして方法1でも方法2でも 消費者と生産者の負担は それぞれ40セントと10セントで変わらない ことがわかりました。驚きです。 この簡単なモデルは 法的には負担していなくてもじつは経済的には 負担している。 見える形では払っていなくても見えない形で払っている。 いっけん盗まれていなくてもほんとうは盗まれている ということを主張しています。
◆参考文献
|