供給曲線（市場）
|
Step3 です。
今回は
個人の供給曲線を横に足し合わせたもの
がマーケット全体の供給曲線であるということを説明します。
いまミキティ 
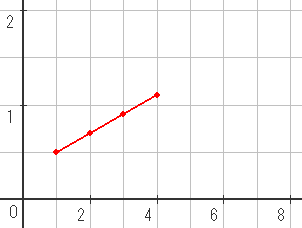
したがって2人は0.5ドルのとき合計2単位、0.7ドルのとき合計4単位、0.9ドルのとき合計6単位、 1.1ドルのとき合計8単位作ることになります。 これをグラフにしたのが ののたん・ミキティペアの供給曲線ということになります。
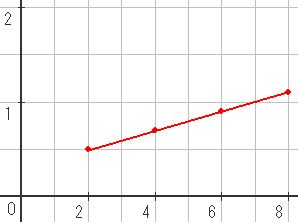
これはののたんのグラフをミキティの分だけ横に移動したものです。 あるいはののたんのグラフとミキティのグラフを横に足し合わせたものです。 以上より個人の供給曲線を横に足し合わせたもの がマーケット全体の供給曲線であるということがわかるとおもいます。 
◆マーケット全体の限界費用曲線 いまののたん・ミキティペアの限界費用曲線 というのもかくことができます。 それが下のグラフです。
これはやはりののたんとミキティの限界費用曲線
を横に加えたものです。（下図）
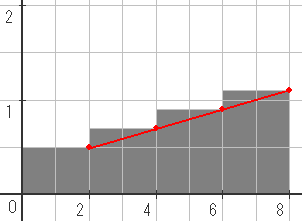
グラフはののたん・ミキティペアのキャンディーを作るコスト（限界費用）が
1単位目： 0.5ドル
ということを表しています。 これは下のように見るとわかりやすいです。 
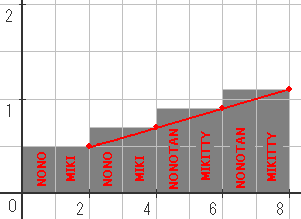
ののたんとミキティのコストをいっしょに積んでいくのですね。 ののたんとミキティの限界費用曲線はやはりののたん・ミキティペアの供給曲線と同じです。 以上より個人の限界費用曲線を横に足し合わせたもの がマーケット全体の限界費用曲線であるということがわかるとおもいます。
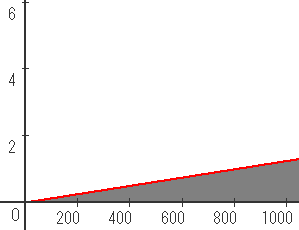
そしてこれはやはりマーケット全体の供給曲線と同じです。
|
もキャンディーの生産者であるとしましょう。
ミキティの供給曲線はののたん 
と同じであるとします。
ミキティは0.5ドルのとき1単位、0.7ドルのとき2単位、0.9ドルのとき3単位、
1.1ドルのとき4単位を作ります。