 独立試行
独立試行
|
パチスロで悩まされるのがハマリの問題です。
回せど回せど当たらない。機械内部から当たり乱数が消失したのではないかと疑念を抱きつつ、それでも回し続ける。挙句の果てには、いったいオレは何をやっているんだろうと、アイデンティティの危機をもたらすのが「ハマリ」です。
今回はその「ハマリ」を解く鍵である独立試行の概念を考えてみたいとおもいます。
独立試行とはその名の通り「互いに影響を与えない試行」ということです。 いわゆる「コインは記憶をもたない」というやつです。 コインを投げたり、サイコロを振ったりすることを「試行」といいます。 一般に同じ試行を繰り返し行なうことを連続試行といいます。 サイコロを続けて振る連続試行においては、1の目が出る確率は毎回 1/6 であり、1つ前の回で1の目が出たか否かには関係しません。一般に n 回の連続試行のどの回においても、ある事象Aの起こる確率が毎回 p であるとき、この試行を独立試行といいます。 独立試行はまた「ベルヌーイ試行」ともよばれます。 また、1の目が出ないことは、この独立試行における余事象であり、その確率は 5/6 です。 一般に独立試行の余事象の確率は 1-p になります。 パチスロをぶんぶん回すことは連続試行であり、独立試行です。 いま、「BIGが当たるか当たらないか」という独立試行を考えます。 BIGが当たる確率を p とします。当たらない確率は 1-p です。 n プレイのハマリとは「 nプレイ試行して、BIGに当たらない」ということです。 いいかえれば「 nプレイ連続してはずれ続ける」ということです。 この確率は (1-p)n です。 また、「 nプレイ試行して、BIGに当たらない」の余事象は「 nプレイ試行して、BIGに当たる」です。 いいかえれば「 nプレイ以内に、BIGに当たる」ということです。 この確率は 1-(1-p)n です。
これらのことをさらに言いかえると、
1-p=q とするとさらに簡単な式になり、 ここで z = 1- y ということに注意してください。 連チャン確率は1からハマリ確率を引いたものということです。 連チャン確率とはいいかえればハマらない確率ということになります。
いまBIG確率が 1/241 とします。つまり p= 1/241 とします。 y = 0.016 という数字は、BIGの 98.4% が 1000 プレイ以内にくることを示しています。そして 1.6% が1000プレイを超えることを示しています。 p = 1/241 の台を 7000 プレイ打つと、平均して 7000*(1/241)=29.0 回 BIGがきます。そこでこのうち平均 29.0*0.016=0.46 回は1000プレイを超えるということです。 したがって2日に1回くらいは、1000プレイハマリを覚悟しなくてはいけません。
ハマリの裏返しが連チャンです。
nプレイ以内連チャン率 z = 1-(240/241)n 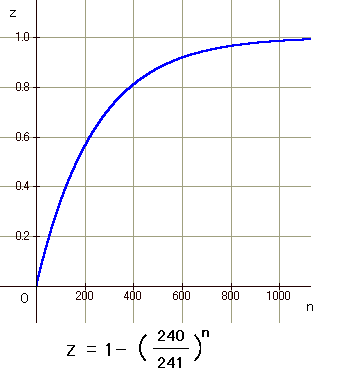 nに n=50, 100, 150 ,・・・などと入れていったのが次の表です。これを見ると「100プレイ以内連チャン率は 34% か」などとわかります。  |
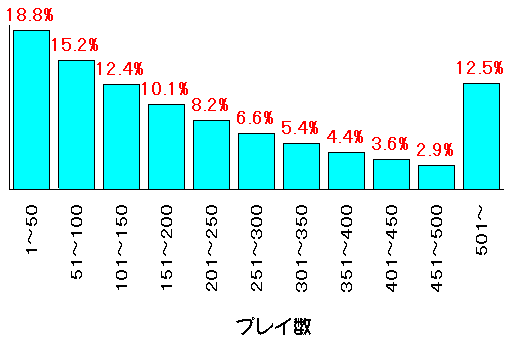
|
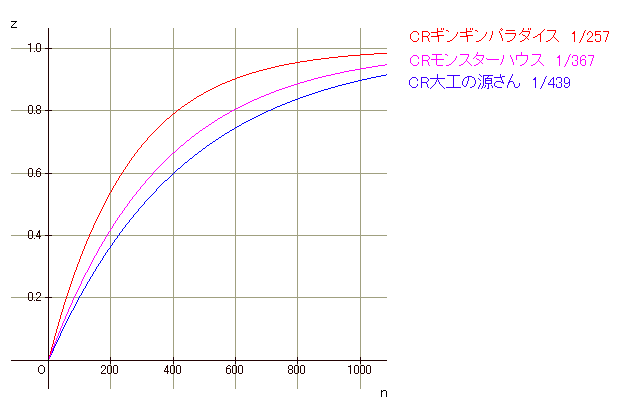
式 z = 1-(1-p)n は当然パチンコでも使えます。p の値をいろいろ変えてみたのが、下の図です。(CRの3大ヒット機種です。
確率 p は設定のある機種については最低設定のものを使っています。)
1から z を引いたのがハマリの確率です。
大工の源さんを見てみると、初当たりの10回に1回は1000回転を超えてしまうことがわかります。
パチンコ史上最もリスクの高かった台です。
|
|
パチスロ・パチンコではオカルト打法なるものが存在します。
確率世界で起こることに耐えられなくなると、人はオカルトウイルスに感染しやすくなります。この「独立試行」の概念はそのウイルスに対抗する一種のワクチンです。
ぜひ定期的に接種しておくべきだとおもいます。

|