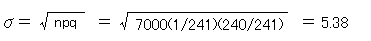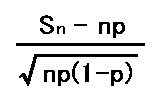二項分布

管理人は「ニューパルサー」の設定5, 6のデータを合わせて76万プレイもっています。日本の個人ではおそらく5本の指に入るだろうとおもいます。 さて、前回までの「独立試行」では、連チャンの可能性あるいはハマリの可能性の求めかたを紹介しました。 今回はその独立試行の考えをもっと進めて、 BIG確率が 1/241 の台を7000プレイ打ったとき、BIGが35回以上出る確率はいくらか というようなことを考えたいとおもいます。 まず、「ベルヌーイ試行」を思い出してください。これは打率 p の打者が3打数でちょうど2安打する確率を求めたのでした。では3打数で2安打以上する確率はいくらでしょうか。 これは＜2安打＞または＜3安打＞の確率なので、和の法則により、 3p2(1-p)＋p3 になります。 上の問題はこれと同じですよね。すなわち、 BIG確率を打率、プレイ数を打数、BIGの回数を安打数と考えればよいわけです。 よって7000打数で35安打以上する確率なので、 ＜35安打＞または＜36安打＞または＜37安打＞または・・・または＜6999安打＞または＜7000安打＞で、これらの確率をそれぞれ求めて足せばよいのですね。 しかし、そんなことができるのでしょうか。 ・・・無理です。 じつは、こういうときに役に立つ数学というのがあるのです。 それが「正規分布」とよばれるものです。独立試行の確率をモデルにした確率変数を 「二項分布」といい、またそれは試行回数が十分に大きければ、「標準正規分布」で近似できることが知られています。 とりあえず実際に計算してみます。なぜこうなるのかは追々詳しく話していきます。 まずはこういう方法があるということだけ知っておいてください。 μ＝ np ＝ 7000(1/241) ＝ 29 考える二項分布はμ＝29 、σ＝5.38 の正規分布で近似できる。 x＝34.5 を標準化すると z＝(34.5-29)/5.38 = 1.0223 求める確率は 0.1533（→ Excel の NORMSDIST 関数で求める） 求める確率は 0.153 ということになります。 注：Excel を使えば、直接、二項分布の確率が求められます。 BINOMDIST 関数を使って求められる確率は 0.1551 で、誤差は 0.0018 です。かなり良い近似であることがわかります。 いったいどういう操作をしているのでしょう。 まず7000プレイ打つと平均29回BIGが当たります。 そして平均を中心にしたばらつき方が図のような曲線で近似できるわけです。 実際は約95％が20〜40回にばらつきます。 面積が累積確率を表すのです。 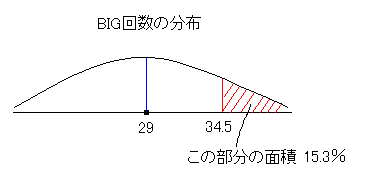35回以上引く確率は、斜線部の面積に等しく、15.3％です。 （補正するので34.5になる）。 また、40回以上引く確率は 0.0255 です。 ただ40回も引くと、BIGの消化時間が長くなり、実際には7000プレイも打ちません。 あくまでも理論値なんですね。 ★ド・モアブル−ラプラスの定理 ベルヌーイ試行に対する中心極限定理はド・モアブル（1667-1754）、ラプラス（1749-1827）によって古くから知られている。 ド・モアブル−ラプラスの定理　　成功の確率が p である n 回のベルヌーイ試行において、 Sn をその成功の回数とすると、 n が十分に大きいとき は近似的に標準正規分布に従う。 ★確率密度関数

★ Excel で二項分布の確率を求めるには BINOMDIST関数（true）を使います。BINOMDIST は binomial distribution （二項分布）の略です。 BINOMDIST(34,7000,1/241,1)　で、最大34回当たる確率を求めます。 BINOMDIST(34,7000,1/241,1) = 0.844882847 BIG回数の分布は＜0回から34回まで＞または＜35回以上＞に分けられるので、 35回以上当たる確率は1からこれを引いて　0.155117153 ★データ パチスロを打つときにプレイ数を数え、下のようなデータを作ります。